FALL
2022 Math 461 --- RINGS AND MODULES
Prerequisite: Math 367 or consent of instructor. Credits: (3-0) 3.
Instructor: Semra Öztürk, M 138, Schedule and office hours are at the address http:/www.metu.edu.tr/~sozkap/aa.pdf.
Catalog Contents: Rings, ideals, isomorphism theorems, group rings,
localization, factor rings. Modules, submodules, direct products, factor
modules. Homomorphisms, classical isomorphism theorems. The endomorphism ring
of a module. Free modules, free groups. Tensor product of modules. Finitely
generated modules over a principal ideal domain.
Grading will be based on two midterms %40 each, one final exam %50, and attendance/class
participation %10.
Exam 1 on Nov 7
Monday, 17:40
Exam 2 on Dec 12
Monday, 17:40
You should
take both of the midterm exams, I will omit the lower grade (even if you
are happy with your first midterm grade you still have to take the second
midterm exam)
Attendance is required,
attendance and class participation will be %10 of the course grade.
Description of the course: This course is
to provide the background for students
who are willing to learn more about rings and modules which are the fundamental mathematical structures
occuring everywhere ! It is good for
everyone but especially for students who are planning to study any
algebra related topics such as algebraic topology, algebraic geometry,
even analysis, or
even machine learning.
This semester I will spend less than half of the semester
on rings and spend more time on modules.
Rings will be a more detailed but
much faster version of some of the topics
you have seen in Math 367, and
Math 116. Modules will be new to
you. They are generalizations of vector
spaces also generalization of abelian groups.
(Modules over group
algebras are examples of groups acting on vector spaces.)
Thus in module
theory linear algebra comes up quite
often. You should be comfortable using
linear algebra to get more out of this course. We will see the primary
decomposition theorem for finitely
generated modules over a Euclidean domain.
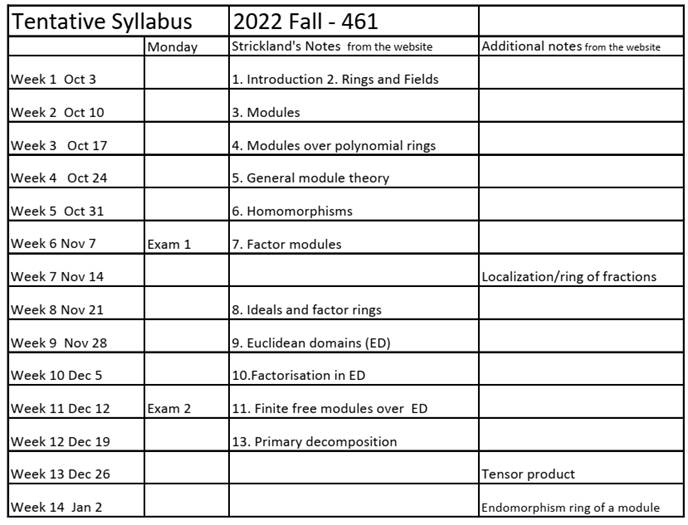
You can print a tentative
syllabus from here.
Textbook : Rather
than the textbooks which are listed below and can be used as
refence material I will use several
lecture notes available online in this semester.
Except for the topics listed below we will use
the notes by Neil P. Strickland
ˇ
Localization/ring
of fractions
ˇ
Ring of endomorphisms of
a module Musil`s or Dummit and Foote`s book below can be used.
ˇ
Tensor products: Tensor
Products Demystified, Tensor product of
abelian groups, Tensor
Product of vector spaces, Notes on Tensor
products by Rich Schwartz
Some textbooks which are used in earlier
semesters can be useful:
1) Introduction to
Rings and Modules, Second Revised Edition, by C. Musili,
Narosa Publishing House, 1994, only Chapters 1--5 ( the
part for rings is too long and the part for modules is too short)
2)
Abstract Algebra by David S. Dummit and Richard M. Foote, Third
Edition, only
the Preliminaries and Chapter 7 .
3) A First Course in
Module Theory by M. E. Keating,
Imperial Clollege Press, only the Chapters 2--9
Further
Inspiring Reading: (UPDATED Nov 21 2022)
The number of homomorphisms from Zn to Zm.pdf
Classification_of_Finite-Finite rings.pdf
A nice set of lecture notes by Mike Prest which covers
more topics than our course content advanced students
may like it,.(Chapters 0,1,2,6 are usefull for this course, at first reading omit Chapters 3, 4, 5)
Supplementary solved exercises
The Arithmetic of Gaussian Integers
Chinese
remainder theorem and its applications, MA Thesis by Jacquelyn Ha Lac
Some solved problems about rings and ideals
Commutative Algebra unfinished notes by N. Strickland
Updated