|
EasyNumerics Software |
|
Optimization
When you select the "Optimization" module from the main menu, the following window appears.
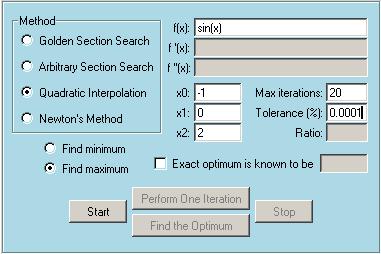
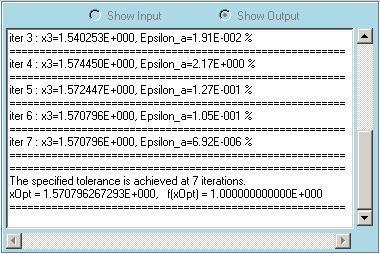
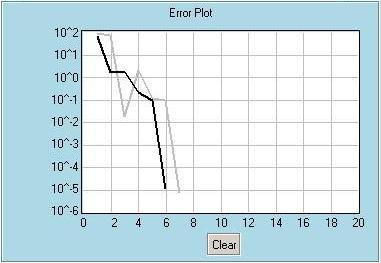
To help understanding how to use this module, some snapshots taken during a sample run are shown below. The first snapshot shows the entries. We will find the first positive optimum point of sin(x) (which is p/2) using the Quadratic Interpolation method. Starting points are specified as x0=-1, x1=0, x2=2 . Note that the interval [x0, x1] must contain only one optimum point and x2 must be in this interval. Maximum number of iterations is selected to be 20 and the tolerance is set to be 10-4. We also tell the program that we are afer a maximum point. Second snapshot shows the Output window, which lists the final answer and the results of the final iterations. It took 7 iterations for the Quadratic Interpolation method to converge. Approximate relative errors are calculated at each iteration. Third snapshot shows the Function Plot window after the first iteration. The black line is the function provided, sin(x). Three black points are the function values at the initial points provided by the user. Gray line is the parabola passing through these three points, and the red point is the maximum of this parabola. Red point is the estimated maximum after the first iteration. Fourth snapshot shows the Function Plot window after the second iteration. After the first iteration a check was performed and one of the black points (x0 in this case) is replaced with the red point (actually with a point corresponding to sin(xred)). Now a new parabola is passed through this new set of black points and its maximum is calculated. The new red point is our new estimation. Fifth snapshot shows the Error Plot window. Gray line is the convergence based on the approximate relative errors (when the exact solution is not provided). Black line is the convergence based on the true relative errors (when the exact solution is provided) As seen approximate relative error plots generally have oscillatory behavior.
Please visit the movies section to watch sample runs of EasyNumerics. |