Hints from Life to AI, edited by Ugur HALICI, METU, 1994

 

 

 

artificial versus natural stereo depth perception

 

Ugur M. Leloglu

TUBITAK-AEAGE, METU

06531, Ankara, TURKEY

lel@tbtk.metu.edu.tr

 

Some cues on stereo vision that are implied by research on natural visual systems are overwieved and then the methods used by computer vision systems for solving the same problem is overviewed. The effect of  those natural cues on computational stereo is discussed.

 

1. Introduction

 

 

Visual perception is an interpretation of 2-dimensional time-varying light information on the retinae to form a spatiotemporal reconstruction of 3-dimensional world. During the long course of evolution, this ability has reached an astonishing complexity, especially, in higher animals. From the "meaningless" sensory input, that is, from a set of activation values of sensory cells, a rich, abstract description of the environment is derived. The recovery of the third dimension information that is lost during the projection on the retinae is vital in this reconstruction process. In human stereo vision system, there are several known ways of estimating the depth like motion, shading, texture and stereo. Although these mechanisms are known in principle, the underlying biological structure and processes are not totally solved yet. Stereo vision is one of the most investigated depth perception mechanisms.

 

 

Figure 1: Eyes are fixated on the farthest of three ballons.

 

The stereo vision is based on the differences between the right and left eye images. Due to the distance between the eyes (interocular distance), the projections of a certain point on the two retinae are at different positions. The difference in these positions is called disparity and its value is related to the distance of the object. In Figure 1 and Figure 2 this process is illustrated schematically. The two eyes are fixated on the farthest of three ballons (Figure 1). That is, the eyes are directed such a way that the images of that ballon are at the centers of both retinae. The resulting left and right images are shown in Figure 2. It is clearly seen that the disparity values are larger for closer ballons. Once, for each point in one of the image, the corresponding point in the other one is determined, the depth of all points can be calculated as a function of the eye vergence.

 

Figure 2: The images formed on left and right retinae of eyes in Figure 1.

 

Our brains do this computation for us continuously and we do not even notice this effort: it is totally unconscious and automatic. To understand how this is possible is subject of several disciplines. Neuroanatomy and neurohistology identify the structures involved in vision in macro and micro scale, respectively. Neurophysiology tries to explain how these structures function. Psychophysics examine how certain visual inputs are perceived under certain conditions.

Cognitive psychology tries to explain the stereo mechanism in a more abstract level than neurophysiology.

 

Besides other reasons, to understand natural stereo vision is useful in constructing similar artificial systems. Such systems have a wide range of application areas (though not all are innocent), so considerable effort is devoted to this area. Any artificial system does not necessarily carry the properties of natural systems as long as it works properly, but the ideas from nature always prove to be powerful.

 

 

2. Problems in Matching

 

To understand why calculating stereo correspondence is not a trivial task, consider a stereo image pair  given in Figure 3 and the light intensity levels of two small image patches from this figure (areas inside the rectangles in Figure 3) as given in Figure 4.

 

 

Figure 3: Pentagon stereo pair (from Prof. Takeo Kanade of Carnegie-Mellon University)

 

The average disparity of 1 pixel is not evident even after a long inspection by eye. The light intensity is coded as binary numbers in computers and coded as frequency of action potentials in human retina, but the very same data is the input of both systems. A simple comparison of intensity values is clearly not sufficient for determining corresponding points. One of the reasons for differences in intensity values is the noise that appears in any sensor either biologic or electronic. Another reason is reflectance properties of most surfaces: the light reflected from the surface depends on the viewing angle. Areas with no significant texture and areas with repetitive texture like a chess table increases the ambiguity. The areas which are seen in one image but occluded in the other are another source of ambiguity because we do not know which areas are occluded before calculating correspondence.

 

Since intensity values change considerably across images, we need some invariant properties for matching. These matching primitives may be edge points, line segments blobs or similar local image properties which can be calculated by simple local processing units. Alternatively, the matching of images can be postponed until monocular recognition of objects in the images. Then recognised objects can be matched easily. After reviewing some facts on natural stereo vision, we will discuss which strategy is used by biological systems and which one is appropriate for computer stereo vision.

 

 

 

 

129  124   132  135  123  130  131  127  127  120  112  123  111  126  147  129

149  142  149  157  142  134  128  128  137  129  125  114  124  136  132  128

169  177  156  159  161  136  126  129  155  158  145  141  166  154  131  129

157  162  156  160  140  129  127  127  133  147  157  172  166  139  131  132

159  147  132  144  131  129  126  135  163  156  159  170  147  131  136  140

146  150  138  133  127  130  125  124  142  143  149  151  129  127  133  152

119  139  139  128  126  123  125  131  131  124  131  129  111  114  118  134

103  113  128  126  126  126  130  149  151  152  143  112  96   105  113  133

108  124  127  125  124  145  157  146  152  168  149  122  117  120  129  152

127  128  124  121  111  129  165  155  149  151  137  130  138  149  143  143

132  126  124  120  110  120  144  167  159  136  130  126  118  144  158  144

128  125  121  107  116  124  123  144  155  134  130  123  104  127  148  148

125  123  115  108  128  140  145  143  133  131  134  147  138  142  143  163

124  122  105  119  151  167  175  150  131  130  137  165  175  163  145  161

126  128  124  135  159  163  161  136  129  127  132  166  173  149  143  141

131  133  137  148  153  162  145  131  128  121  126  149  149  134  133  149

 

a) Intensity levels of left patch

 

139  160  139  125  134  136  134  133  120  128  113  113  137  144  132  125

148  150  155  150  136  135  133  148  147  146  122  144  154  138  136  130

178  154  160  155  136  135  126  145  163  147  152  177  159  140  136  133

154  151  159  139  137  132  126  140  152  159  173  162  142  142  137  137

147  134  146  136  135  129  135  167  156  155  165  143  139  139  144  154

152  142  135  134  129  128  133  145  133  151  154  134  135  136  152  172

140  141  134  133  125  140  155  139  131  138  133  124  119  113  130  162

133  134  132  130  125  135  162  160  156  145  129  118  114  115  130  141

134  132  131  123  150  168  150  160  167  149  137  132  137  132  151  145

133  132  128  115  138  170  154  158  144  137  138  141  161  153  140  134

134  131  126  121  135  144  159  163  139  140  130  113  143  162  142  129

132  125  116  126  132  131  138  146  139  139  128  122  139  148  151  154

128  118  126  143  155  155  152  138  138  138  154  159  159  147  163  170

128  112  129  153  159  161  144  138  136  133  162  181  161  146  146  173

131  132  143  151  157  149  138  137  129  137  166  166  146  148  140  149

137  133  141  127  151  140  137  135  129  140  160  150  140  150  168  144

 

b) Intensity levels of right patch

 

 

Figure 4: Intensity levels of two patches shown in Figure 3.

 

3. Natural Stereo Vision

 

Although a complete theory of biological stereo vision is not built yet, there is a large body of information obtained through neurophysiological and psychological research on steropsis. Here, some facts on human stereo vision which are closely related to computer stereo vision will be briefly presented. Interested reader is recommended to refer [Hubel88], [Bruce90] and [Splillmann90] for detailed information.

 

The speed of human stereopsis

 

A very remarkable feature of human stereopsis is its speed: it takes about 200 msecs from presentation of the stimulus to the occurrence of depth perception [Yeshurun89]. That duration is very close to the time needed for the information on the retinae to reach to the visual cortex via the visual pathway.

 

Stereopsis is a Low-Level Process

 

Stereopsis is a low level process; that is, it does not require recognition or any abstract understanding of the image. It was first demonstrated by Julesz that [Julesz60] stereopsis survives in the absence of any monocular cue such as texture, a priori knowledge on the shapes and sizes of objects, shading, etc. Figure 5 is an example of random dot stereograms which was invented by Julesz. One can see the floating square above the background when he fixates his eyes at a nearer point in such a way that the two images overlap in the centre. But this phenomenon does not imply that other depth cues do not effect the stereo process. On the contrary, there is strong evidence that presence of monocular depth cues facilitates stereo vision.

 

 

Figure 5: A random-dot stereogram

 

 

Limited Fusional Area

 

Only the surfaces within a specific disparity interval, so-called Panum's fusional area, can be fused. The extent of this range is measured between 10-40 minutes of arc depending on the data used. There is evidence that this range is larger for inputs with low frequency content compared to high frequency inputs [Marr82] [Schor84].

 

Effect of Contrast

 

It was shown by Julesz that [Julesz71] changes in the magnitude of the contrast across the images does not destroy stereopsis, but a change in the sign of contrast makes fusion of images impossible [Julesz60].

 

Hyperacuity

 

Even though the average distance among the light-sensitive cells of the retina (cones), is about 20-30 seconds of arc at the fovea where those cells are densest, the disparity differences down to 2 seconds of arc are detectable by the human visual system [Morgan82]. But this hyperacuity drops drastically for non-zero disparities [Badcock85].

 

Gradient Limit

 

If the rate of change in disparity, that is, the disparity gradient, exceeds a certain limit the images cannot be fused and objects appear as double (diplopia) [Burt80].

 

Binocular Cells in Visual Cortex

 

Although there is some interaction of information from both eyes on the way from retinae to cortex, the first place where cells differentially sensitive to binocular disparity are observed is the visual cortex in cats and monkeys. A considerable proportion of the cells at visual cortex are binocularly sensitive [Hubel62].

 

Ocular Dominance

 

Binocularly sensitive cells can be classified as balanced or unbalanced according to the type of their sensitivity [Poggio77]. Balanced cells respond equally to stimuli from each eye, but respond very strongly when stimulated binocularly. Unbalanced cells either respond stronger to one eye or exhibit a complex ocular dominance pattern.

 

A certain layer of the visual cortex (layer 4) is organised in ocular dominance columns. These vertical strips which are 1 mm thick in monkeys and 2 mm thick in humans respond alternatingly to left eye and right eye. Binocular cells are located above and below these monocular cells.

 

Orientation Selectivity

 

Almost all of the cells in visual cortex exhibit orientation selectivity at various angles. But most of them respond best to bars oriented within 20 degrees from the vertical [Poggio77].

 

 

Frequency Selectivity

 

Another important property of these cells is their frequency selectivity. The range of optimal spatial frequencies range from 0.3 to 3 cycles/degree in cats and 2 to 8 cycles/degrees in monkeys [Bruce90]. The bandwidth of cells in the average is a little bit larger than one octave. The constancy of relative bandwidths over scales can be justified by the statistics of natural images [Field87]. There is almost constant energy in all channels, because the amplitude spectrum of natural images generally fall off with 1/f.

 

Receptive Fields Types

 

Receptive field is the activation pattern of a cell as a function of stimulus position on the retina. According to the pattern of their receptive fields the cells in the visual cortex are classified as simple and complex cells [Schiller76a] . Simple cells have smaller receptive fields and low spontaneous activity. Some parts of their receptive field respond the onset of the stimulus while some parts respond to the offset. On the contrary, complex cells respond both the onset and the offset. They have larger receptive fields and greater spontaneous activity.

 

Binocular Sensitivity Types

 

According to their binocular sensitivity, the cells in the visual cortex are classified into four groups by Poggio and Fischer [Poggio77] as tuned excitatory (TE), tuned inhibitory (TI), near and far. TE cells are excited by stimuli at the fixation distance. If the stimulus is disparate more than 0.1 degrees then the cell activities are suppressed, that is, these cells are sharply tuned to zero disparity. The response pattern of TI cells as a function of disparity is the reverse of, but is not as sharp as, that of the TE cells. Near cells are sensitive to stimuli near than the fixation distance and far cells are visa versa. Among these cell groups only TE cells are ocularly balanced. Later, other kinds of cells are also identified and it is claimed that types according to binocular sensitivity belong to a continuum rather than discrete groups [Freeman90].

 

Modelling Simple Cells

 

The monocular receptive fields of simple cells are well described by Gabor functions [Marcelja80] [Daugman80] which are filters limited in both space and frequency. Gabor filters will be discussed in detail later in this article. There exists evidence that simple cells are found in pairs with an approximate phase difference of 90 degrees [Pollen81] which may compute real and imaginary parts of a complex Gabor filter. The integration of data from monocular receptive fields is modelled as linear summation by Ohzawa and Freeman [Ohzawa86] based on neurophysiological experiments. Nomura et al. [Nomura90] proposed a similar modelling where linear summation is followed by a non-linear smoothed thresholding function. This model predicts largely the binocular behaviour of cells in the striate cortex. Freeman and Ohzawa observed that the phase difference sensitive responses of simple cells are not disturbed by large contrast differences across right and left eyes. Considering this observation, they proposed a monocular contrast gain mechanism that keeps the effect of contrast almost constant.

 

Coarse-to-Fine Structure

 

There is evidence that data from low-frequency channels constrain the matching at high frequencies. Wilson et al. [Wilson91] found that channels more than 2 octaves apart process independently, but closer channels interact. Low-frequency signals affect fusion in high-frequency channels but not vice versa. Watt [Watt87] also concludes, after a series of experiments, that the human visual system uses a coarse-to-fine strategy.

 

4. Computer Stereo Vision

 

The Matching Primitives

 

In the beginning, we considered the problem of what to choose for matching across images. The fact that human stereopsis can survive without monocular recognition, is very comforting for computer stereo research, since general recognition performance of computer vision's state-of-the-art is very weak.

 

We know that raw intensity values are not appropriate as matching primitives while recognised objects are not available. What we need, at this point, is matching the primitives that are more abstract and invariant than intensity values that can be determined without any help from top-down processes. We can group such primitives that currently used in computer vision into two rough groups. The first consists of features like edges, corners, blobs etc. which can be detected using local intensity values. The second group, area-based properties, are functions of intensity values that can be calculated at almost every point of an image.

 

Features

 

Image features which are chosen for matching are high interest points or point sets like edgels, edge segments or intervals between edges. The features can be localised very accurately (generally with sub-pixel resolution), so the accuracy of computed disparity is also high. Features generally correspond to physical boundaries of objects, surface markings or other physical discontinuities, so provide valuable depth information. Features are typically sparse, that is, they occupy only a very low percentage of an image. This speeds up processing, but disparities at non-feature points should be interpolated.

 

 

Figure 6: Laplacian-of-Gaussian operator

 

Use of features for stereo matching is biologically plausible, because cells sensitive to edges and corners are observed in the visual system. Based on the properties of some cells in the lateral geniculate, Marr and Hildreth [Marr80] proposed the zero-crossings of Laplacian-of-Gaussian (LoG) filtered images for edge detection. The LoG operator (Figure 6)

 

 

 

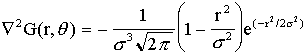
which is Gaussian smoothing followed by a second derivative operation, has several useful properties. The scale factor , which is the standard deviation of the Gausian, is inversely proportional to the average density of edges. Besides, even large convolutions can be calculated quickly by either approximating the LoG by a difference-of-Gaussians function or by decomposing the LoG. The disadvantage of LoG is the displacement of edges with growing . After Marr [Marr82] a number of researchers used zero-crossing edges as matching primitives. The direction of the edge is approximated as the direction of the gradient of the filtered image. Only edgels with the same sign and with roughly the same orientation are considered as possible matches. This is in accordance with the psychophysical observaation that images with opposite contrast cannot be fused.

 

More abstract image features are edge segments, either linear line segments or curves. The edgels are not matched individually but grouped into segments. This grouping can be performed by using Gestalt rules. Grouping reduces the number of possible matches significantly. Besides, one can define similarity measures of two edge segments using their length, orientation, curvature, strength, coordinates of edge points, average intensity or intensity slope at each side etc.

 

Area-Based Primitives

 

Area properties are those which are available at almost every point in an image. The simplest area property is the image intensity which is not appropriate for stereo matching due to its sensitivity to noise as well as to photometric variation. Another simple primitive is the spatial derivative of intensity that is less sensitive to photometric variation, but this measure is too  sensitive to noise.

 

A common way to match areas directly is to find correlations of areas from left and right images. The cross-correlation and normalized cross-correlation at position (i,j) of the right image with disparity d are

and

 

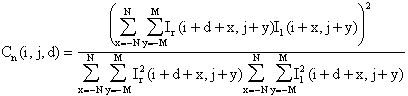
respectively. There are several other correlation-like measures of which the most frequently used one is the sum of squared differences:

.

 

Although correlation techniques are successful at textured areas, they fail around depth discontinuities, since the area inside the correlation window belongs to at least two different surfaces at different depths, so the window does not match totally at any disparity value. They also suffer from disparity gradients because one of the signals is scaled compared to other. Besides, the accuracy obtained is lesser when compared to feature-based matches. Another drawback of the correlation technique is its computational complexity. As the size of the correlation window gets larger, the computational complexity and the uncertainty in disparity increase as well as problematic regions near discontinuities get larger, but, match becomes more robust to noise.

 

Another dense property to match is local frequency components [Clark86] [Sanger88] [Fleet91] [Westelius92] [Weng93] [Nomura93]. The Fourier theorem states that when a function f(x) with Fourier transform F(u) is shifted by an amount of x then the Fourier transform of the shifted function  is , so a shift in the spatial domain corresponds to a phase shift in the frequency domain. If the left view had been a shifted version of the right view it would have been possible to determine the amount of shift from the phase of the Fourier transforms of both images. But since the shift, i.e. the disparity, is different in various regions of the images, one needs a local frequency filter to determine the phase differences. A natural choice for such a function is the Gabor filter [Gabor46] which is a bandpass filter with limited spatial width:

 

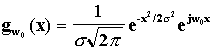
whose Fourier transform is

 

where the product  is 1 which is the theoretical minimum of any linear complex filter [Gabor46]. This choice is also biologically plausible since the receptive fields of simple cells are not statistically distinguishable from Gabor filters [Marcelja80]. Besides, simple cells are found in pairs with an approximate phase difference of 90 degrees [Pollen81] and this justifies the use of complex filters. If the ratio of the spatial width to the period, , is held constant, then the shape of the filter and the relative bandwidth given by

 

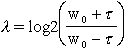
in octaves remain unchanged. Figure 7 shows the real and imaginary parts of a Gabor filter with a bandwidth of 1 octave. The 2-dimensional extension of the filter is

.

 

 

 

 

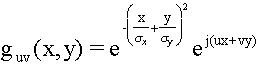Figure 7: The real and imaginary parts of a Gabor filter with a bandwidth of 1 octave.

 

 

Note that the filter is separable, so computational complexity is reduced from  to . The filtered versions of right and left images  and  are

 

and

 

.

 

So that the Gabor filtered image is a band-pass signal, it can be modelled (in 1-D for simplicity) as [Fleet91]

 

 

where  is the centre frequency equal to the frequency of the filter. The local frequency is defined as [Papoulis65]  where . If we assume perfect sinusoids, that is,  then we can estimate the disparity as [Sanger88]

 

.

 

Since the bandwidth of the filter is non-zero,  may vary around zero and disturb the linearity. But in real images with sufficient texture the phase is almost linear over the image except some regions. Fleet et al. [Fleet91] showed that the bandpass phase is not sensitive to typical distortions that exist between right and left images.

 

Note that the phase measurements give the disparity directly, so a search is not performed for the best fit, because of this phase-based techniques are sometimes called ``correspondenceless''. It is worth mentioning that matching phases is a general case of matching zero-crossings because the zero-crossings of band-pass filters such as LoG correspond roughly to level curves at  of the phase signal. Another advantage of the phase-measurements is that they provide sub-pixel measurements without explicitly reconstructing the signal between pixels. This hyperacuity is also in accordance with biological findings.

 

Phase measurements are valid within a limited range of disparity because of the wrap-around problem: we measure only the principal component of the phase in the range , so a filter of fundamental frequency  signals only disparities of  to .

 

Nomura [Nomura93] introduced a fundamental equation for binocular disparity,

 

 

where o is the eye position, I is the intensity and d is the disparity. This equation is a variation of the gradient model of optical flow field. Substituting Gabor filtered image in place of I, he obtained

 

 

Besides he showed that the terms other than d can be approximated as linear combinations of far, near and tuned inhibitory type simple cells.

 

Another area-based method that takes its flavour from natural stereo vision is the cepstral filtering approach of Yeshurun and Schwartz [Yeshurun89]. Cepstral filtering is a Fourier transformation followed by a logarithm and an inverse Fourier transform. Yeshurun and Schwartz append left image, l(x,y) to the left of right image, r(x,y). Assuming that the width of the patches is D and r(x,y) is equal to l(x-d,y) where d is the disparity to be computed, the compound image f(x,y) can be written as

 

 

with the Fourier transform

 

.

 

When we take the logarithm of F(u,v), the product becomes a sum:

 

 

Taking the Inverse Fourier Transform, we obtain

 

.

 

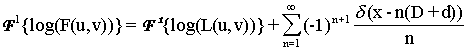Thus, we can find the disparity of the patch by locating the largest delta function. Ocular dominance columns in the visual cortex that correspond to alternating image patches from right and left retinae have great similarity with the above method. Besides, the width of ocular dominance columns is in accordance with the Panum's fusional area. The authors also claim that this cepstral filter can be implemented using a set of bandpass filters similar to those found in the visual cortex, so this approach is biologically plausible.

 

Constraints

 

Since the combinations of all possible matches reach an enormous number, some a priori data is needed about the disparity field. The assumptions made are imposed on the algorithms as constraints. Every stereo algorithm uses some of these constraints implicitly or explicitly.

 

Smoothness

 

Marr and Poggio [Marr76] stated that matter is cohesive, that is,

 

"it is separated into objects, and the surfaces of objects are generally smooth in the sense that the surface variation due to roughness cracks , or other sharp differences that can be attributed to changes in distance from the viewer, are small compared with the overall distance from the viewer"[Marr82].

 

The disparity field produced by such surfaces is smooth everywhere except at object boundaries, which occupy only a small portion of an image. Considering this fact, the computed disparity field is forced to be as smooth as possible. Under the smoothness assumption, ill-posed stereo problem has a unique solution. This constraint is related to regularization theory that is a branch of mathematics dealing with ill-posed problems [Poggio85]. Blind use of the smoothness constraint can cause problems at depth discontinuities. A method proposed to avoid smoothing of the disparity field at and near these areas is using line processes where the smoothness constraint is broken.

 

A weaker form of the smoothness constraint is the figural continuity constraint that was first exploited by Mayhew and Frisby [Mayhew81]. This constraint implies smooth variation of disparity along edges, because the edgels on the same edge segment are assumed to belong to the same object and this assumption is almost always valid. Note that the figural continuity constraint is automatically satisfied when contours are used as matching primitives, so the above correction cannot be applied.

 

Smoothness constraint can also be expressed as a gradient limit on disparity that is known to be used in human stereopsis. Generally, the support from a neighbouring match to a potential match is inversely scaled by the disparity gradient between the two matches [Prazdny85].

 

Opaqueness

 

This assumption is violated if there are semi-transparent surfaces in the image, but this is very rare in natural images except objects like fence or bush that occludes background partially. In case of transparency, continuity constraint is not applicable, since the disparity field switches frequently between background and foreground. Human visual system can cope with transparencies without difficulty. To handle transparency as well as discontinuities at object boundaries, Prazny introduced the coherence principle that states that the world is made of (either opaque or transparent) objects each occupying a well defined 3D volume. So:

 

"a discontinuous disparity may be a superposition of a number of several interlaced continuous disparity fields each corresponding to a piecewise smooth surface" as a result "Two disparities are either similar, in which case they facilitate each other because they possibly contain information about the same surface, or dissimilar in which case they are informationally orthogonal, and should not interact at all because they potentially carry information about different surfaces" [Prazdny85].

 

He proposed the support function

 

 

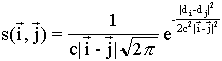
where  is the support from the neighbouring point  to point . Among possible matches at point  only the one with minimum disparity difference  is used in calculation of support. The term  on the exponent is the disparity gradient so the support function imposes a disparity gradient limit implicitly.

 

Orderedness

 

Assume a point A, and a point B that is right to A match points A' and B' in the other image. Then, this constraint states that B' cannot be at the left side of A'. Resulting disparity constraint violates this assumption if the disparity difference between a figure and its background is larger than the width of the figure in the image. Such objects, like columns, ropes etc. are rare in natural images, so this constraint is frequently used to reduce ambiguity. Human visual system also prefers order-preserving solutions [Weinshall89].

 

Uniqueness

 

This constraint states that a point in one image matches only one point in the other image, that is, the disparity field is a single valued function. In stereo pairs involving only opaque surfaces, this constraint greatly reduces the number of possible solutions. If human visual system uses this constraint or not is a controversial problem since there is evidence for both use of this constraint [Weinshall89] and for existence of multiple matches [Pollard90].

 

Compatibility

 

If point A in the right image matches point B in the left, the point B matches point A. Some researchers calculate right and left image disparities independently and then check for compatibility across the field to eliminate false matches. Figure 8 shows valid and invalid matches across two lines schematically where circles and arrows represent pixels and matches, respectively.

 

Epipolarity

 

Affine transformations are applied to the images such that the epipolar lines are collinear with image rows. The determination of the epipolar line reduces the search space to one-dimension, while the alignment with image rows greatly simplifies the search. In human visual system, this constraint is satisfied once both eyes are fixated on the same point, but still small vertical disparities remain due to the perspective projection onto the retinae.

 

 

 

Figure 8: Matches between rows R and L violating a) the uniqueness constraint,

b) the compatibility constraint and c) the orderedness constraint.

d) A valid matching field with 2 occluded pixels in row R.

 

Limited Disparity Range

 

In accordance with Panum's fusional area, the disparity range in which a match is searched for is determined a priori. Sometimes, even when the epipolarity constraint is used, a small vertical disparity range is allowed to compansate for inexact registration.

 

Strategies

 

Once matching primitives are decided and constraints are set, we face a very large problem. A multi-dimensional space is to be searched for (in some sense) the best solution which satisfies all constraints. Since to visit all states for the best solution is impractical, if not impossible, we need to employ heuristics to reach the best or at least a good solution.

 

Multi-channel analysis

 

The existence of different band-pass frequency channels in the vertebrate visual cortex led some researchers to use frequency filters in stereo algorithms. Gaussian smoothing and Gabor-like filters are mostly used in band-pass filtering. As the channel gets coarser (low-frequency), the size of the required masks gets larger, so the computational cost of the filters increases. An equivalent and simpler method is to smooth the image using a Gaussian kernel and to subsample it successively. This way, a Gaussian image pyramid with various resolutions is formed. Usually a spacing of one octave between the channels is used which leads to resolutions of half of the finer channel (i. e., 256x256, 128x128, 64x64). A more rapid way to form the image pyramid is image consolidation which replaces four adjacent pixels with one pixel having the intensity of average of the four pixels. Consider an n by n stereo pair with disparity range m. If integer disparity values are used there are  possible solutions to the problem, while the number of possible solutions in the coarser channel is . The accuracy of the result is half of the coarser channel. But we can use this result to constrain the solution in the next finer

 

 

 

 

Figure 9: Coarse-to-fine control strategy.

 

channel. This strategy is called coarse-to-fine analysis (See Figure 9) and is very popular in stereo research. Besides the computational savings, this method generally leads more accurate final results.

 

The disadvantage of the method is the spreading of any error in a coarse level to finer levels. Also this methods assume spectral continuity. This approach is explained in the next subsection. The alternative multi-channel approach to coarse-to-fine analysis is to process each channel independently and to combine subsequently.

 

Integrating with Other Vision Modules

 

It is well known that human visual perception owns its power to integration of information from a variety of sources such as motion, shading etc. Computer vision maturing in each of such methods now is in the way of building more complete vision systems integrating those modules.

 

Fusing motion and stereo was considered by a number of researchers [Mutch86] [Waxman86] [Li93]. If we know the disparity field or optical flow for a sequence of stereo images, it is easier to compute the other one. Besides, the discontinuities of optical flow are generally also depth discontinuities. So one of them is computed first and is used to guide the other. But Toborg and Hwang [Toborg91] calculated stereo disparity, optical flow and intensity contours simultaneously and co-operatively. They demonstrated the effectiveness of integrating visual modules on synthetic images.

 

Other visual cues used with stereopsis include shape-from-shading [Thompson93] [Grimson84] [Bulthoff88] and shape-from-texture [Moerdler88]. Also, active systems which seek for useful additional information by controlling camera parameters are used more and more frequently [Ahuja93] [Coombs92] [Krotkov93] [Yuille90].

 

5. Conclusions

 

Natural evolution seem to find the optimum solution for perception of the environment. But the solution is optimum in terms of the needs of the species and the available "hardware" of biological systems, so the way they solve perceptual problems may not be appropriate for machine vision. Nevertheless the information obtained through the study of these systems proved to be useful and guiding for design of computer vision systems. This result may also be generalized to other kinds of information processing systems. As the biological basis of perception and cognition is understood better, more powerful information processors can be built.

 

References

 

[Ahuja93] Narendra Ahuja and A. Lynn Abbott, "Active Stereo: Integrating Disparity, Vergence, Focus, Aperture, and Calibration for Surface Estimation", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 15, no. 10, 1007-1029, October 1993.

[Badcock85] David R. Badcock and Clifton M. Schor, "Depth-Increment Detection Function for Individual Spatial Channels", Optical Society of America A, vol. 2, no. 7, 1211-1216, July 1985.

[Bruce90] Vicki Bruce and Patrick Green, Visual Perception: Physiology, Psychology and Ecology, Lawrence Erlbaum Associates, Hove, UK, 1990.

[Bulthoff88] Heinrich H. Bulthoff and Hanspeter A. Mallot, "Integration of Depth Modules: Stereo and Shading", Optical Society of America A, vol. 5, no. 10, 1749-1758, 1988.

[Burt80] Peter Burt and Bela Julesz, "A Disparity Gradient Limit for Binocular Vision", Science, vol. 208, 615-617, May 1980.

[Clark86] J. J. Clark and P. D. Lawrence, "A Theoretical basis for Diffrequency Stereo", Computer Vision, Graphics and Image Processing, vol. 35, 1-19, 1990.

[Cochran90], Steven Douglas Cochran, Surface Description from Binocular Stereo, PhD. Thesis, School of Engineering, University of Southern California, November 1990.

[Coombs92] David John Coombs, Real-time Gaze Holding in Binocular Robot Vision, PhD. Thesis, Department of Computer Science, University of Rochester, June 1992.

[Daugman80] J. G. Daugman, "Two-Dimensional Spectral Analysis of Cortical Receptive Field Profile", Vision Research, vol. 20, 847-856, 1980.

[Field87] David J. Field, "Relations Between the Statistics of Natural Images and the Response Properties of Cortical Cells", Optical Society of America A, vol. 4, no. 12, 2379-2394, December 1987.

[Fleet91] David J. Fleet, Allan D. Jepson, Michael R. M. Jenkin, "Phase-Based Disparity Measurement", CVGIP: Image Understanding, vol. 53, no. 2, 198-210, March 1991.

[Freeman90], Ralph D. Freeman and Izumi Ohzawa, "On the Neurophysiological Organization of Binocular Vision", Vision Research, vol. 30, no. 11, 1661-1676, 1990.

[Gabor46] D. Gabor, "Theory of Communication", Journal of IEE, vol. 93, 429-459, 1946.

[Grimson84] W. E. L. Grimson, "Binocular Shading and Visual Surface Reconstruction", Computer Vision, Graphics and Image Processing, vol. 28, 19-43, 1984.

[Hubel62], David H. Hubel and T. N. Weisel, "Receptive Fields, Binocular Interaction and Functional Architecture in the Cat's Visual Cortex", Journal of Physiology, London, vol. 160, 106-154, 1962.

[Hubel88], David H. Hubel, Eye, Brain and Vision, Scientific American Library, New York, USA, 1988.

[Julesz60] Bela Julesz, "Binocular Depth Perception of Computer Generated Patterns", Bell Systems Technical Journal, vol. 39, 1125-1162, 1960.

[Julesz71] Bela Julesz, Foundations of Cyclopean Perception, The University of Chicago Press, Chicago, 1971.

[Krotkov93] Eric Krotkov and Ruzena Bajcsy, "Active Vision for Reliable Ranging: Cooperating Focus, Stereo, and Vergence", International Journal of Computer Vision, vol. 11, no. 2, 187-203, 1993.

[Li93] Lingxiao Li and James H. Duncan, "3-D Translational Motion and Structure from Binocular Image Flows", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 15, no. 7, 657-667, 1993.

[Marcelja80] S. Marcelja, "Mathematical Description of the Responses of Simple Cortical Cells", Optical Society of America A, vol. 70, 1297-1300, 1980.

[Marr76] David Marr and T. Poggio, "A Cooperative Computation of Stereo Disparity", Science, vol. 194, 283-287, 1976.

[Marr80] David Marr and E. Hildreth, "Theory of Edge Detection", Proceedings of Royal Society of London B, vol. 207, 187-217, 1980.

[Marr82] David Marr, Vision, W. H. Freeman and Company, New York, 1982.

[Mayhew81] John E. W. Mayhew and John P. Frisby, "Psychophysical and Computational Studies towards a Theory of Human Stereopsis", Artificial Intelligence, vol. 17, 349-385, 1981.

[Moerdler88] M. L. Moerdler, "The Integration from Stereo and Multiple Shape-from-Texture Cues", Image Understanding Workshop, 786-793, April 1988.

[Morgan82] M. J. Morgan and R. J. Watt, "Mechanisms of Interpolation in Human Spatial Vision", Nature, vol. 299, 553-555, October 1982.

[Nomura90] M. Nomura and G. Matsumoto and S. Fujiwara, "A Binocular Model for the Simple Cell", Biological Cybernetics, vol. 63, 237-242, 1990.

[Nomura93] Masahide Nomura, "A Model for Neural Representation of Binocular Disparity in Striate Cortex: Distributed Representation and Veto Mechanisms", Biological Cybernetics, vol. 69, 165-171, 1993.

[Mutch86] K. M. Mutch, "Determining Object Translation Information Using Stereoscopic Motion", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 8, no. 6, 750-763, 1986.

[Ohzawa86] Izumi Ohzawa and Ralph D. Freeman, "The Binocular Organization of Simple Cells in the Cat's Visual Cortex", Journal of Neurophysiology, vol. 56, no. 1, 221-242, July 1986.

[Papoulis65] A. Papoulis, Probability, Random Variables and Stochastic Process, McGraw-Hill, Singapore, 1965.

[Poggio77] G. F. Poggio and B. Fischer, "Binocular Interaction and Depth Sensitivity in Striate and Prestriate Cortex of Behaving Rhesus Monkey", Journal of [Pollen81] Daniel A. Pollen and Steven F. Ronner, "Phase Relationships Between Adjecent Simple Cells in the Visual Cortex", Science, vol. 212, 1409-1411, June 1981. Neurophysiology, vol. 40, no. 6, 1392-1405, November 1977.

[Poggio85] T. Poggio, V. Torre and C. Koch, "Computational Vision and Regularization Theory", Nature, vol. 317, no. 26, 314-319, September 1985.

[Pollard90], Stephen B. Pollard and John P. Frisby, "Transparency and the Uniqueness Constraint in Human and Computer Stereo Vision", Nature, vol. 347, no. 11, 553-556, October 1990.

[Pollen81] Daniel A. Pollen and Steven F. Ronner, "Phase Relationships Between Adjecent Simple Cells in the Visual Cortex", Science, vol. 212, 1409-1411, 19 June 1981.

[Prazdny85] K. Prazdny, "Detection of Binocular Disparities", Biological Cybernetics, vol. 23, no. 5, 93-99, 1985.

[Sanger88] T. D. Sanger, "Stereo Disparity Computation Using Gabor Filters", Biological Cybernetics, vol. 59, 405-418, 1988.

[Schiller76a] Peter Schiller and Barbara L. Finlay and Susan F. Volman, "Quantitative Studies of Single-Cell Properties in Monkey Striate Cortex. I. Spatiotemporal Organization of Receptive Fields", Journal of Neurophysiology, vol. 39, no. 6, 1288-1319, November 1976.

[Schor84] C. Schor, I. Wood and J. Ogawa, "Binocular Sensory Vision is Limited by Spatial Resolution", Vision Research, vol. 24, 661-665, 1984.

[Splillmann90] L. Splillmann and J. S. Werner, editors, Visual Perception: the Neurophysiological Foundations, Academic Press, Inc., New York, USA, 1990.

[Thompson93] Clay Matthew Thompson, Robust Photo-Topography by Fusing Shape-from-Shading and Stereo, PhD. Thesis, Massachusets Institute of Technology, February 1993.

[Toborg91] Scott T. Toborg and Kai Hwang, "Cooperative Vision Integration Through Data-Parallel Neural Computations", IEEE Transactions on Computers, vol. 40, no. 12, 1368-1379, 1991.

[Watt87] R. J. Watt, "Scanning from Coarse to Fine Spatial Scales in the Human Visual System After the Onset of a Stimulus", Optical Society of America A, vol. 4, no. 10, 2006-2021", October 1987.

[Waxman86] A. M. Waxman and J. H. Duncan, "Binocular Image Flows: Steps Toward Stereo-Motion Fusion", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 8, no. 6, 715-731, 1986.

[Weinshall89] Daphna Weinshall, "Perception of Multiple Transparent Planes in Stereo Vision", Nature, vol. 341, no. 26, 737-739, October 1989.

[Weng93] J. J. Weng, "Image Matching Using the Windowed Fourier Phase", International Journal of Computer Vision, vol. 11, 211-239, 1993.

[Westelius92] C.-J. Westelius, Preattentive Gaze Control for Robot Vision, PhD Thesis, Department of Electrical Engineering, Linköping University, 1992.

[Wilson91] Hugh R. Wilson and Randolph Blake and D. Lynn Halpern, "Coarse Spatial Scales Constrain the Range of Binocular Vision on Fine Scales", Optical Society of America A, vol. 8, no. 1, 229-236, January 1991.

[Yeshurun89] Yehezkel Yeshurun and Eric L. Schwartz, "Cepstral Filtering on a Columnar Image Artchitecture: A Fast Algorithm for Binocular Stereo Segmentation", IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 11, no. 7, 759-767, July 1989.

[Yuille90] Alan Yuille and Davi Geiger, "Stereo and Controlled Movement", International Journal of Computer Vision, vol. 4, 141-152, 1990.

 

contents                                     home