H. Levent Akin

Department of Computer Engineering,

Bogazici University, 80815-Bebek, Istanbul, TURKEY

E-Mail: akin@boun.edu.tr

Evolutionary algorithms are based on natural selection and genetics. A variety of evolutionary computational models have been proposed. Common to all is the concept of simulating evolution of individual structures using genetic operators such as selection, mutation, reproduction, and recombination. Although around for more than 30 years in one form or another, in the last five years evolutionary algorithms have become widely accepted as practical, robust optimization and search methods. In this survey, we discuss four variants of evolutionary algorithms, namely, genetic algorithms, evolutionary strategies, evolutionary programming,  and  genetic programming. Some interesting applications of evolutionary algorithms are also presented.

1. Introduction

In nature, there is a competition going on for the scarce resources. Only the individuals which are more fit survive. The capability to adapt to a changing environment is one of the determining factors of fitness. The features of the individuals which help its survival are determined by the contents of its genes. The sets of genes that control the features are called the chromosomes.

Evolution is driven by the joint action of natural selection and the recombination of genetic material. Due to natural selection the fittest individuals dominate the others for food, space and mates and survive. One implicit effect of this process is that since they are the ones that can reproduce, it leads to the survival of the fittest genes.

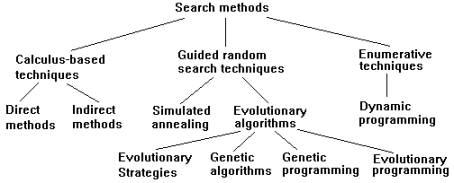
Although around for more than 30 years in one form or another [1, 2, 3], in the last five years evolutionary algorithms have become widely accepted as practical, robust optimization and search methods [4, 5]. Search methods can be grouped into three classes [3, 6].

Figure 1. A taxonomy of search methods.

Evolutionary algorithms are based on natural selection and genetics. A variety of evolutionary computational models have been proposed. Common to all is the concept of simulating evolution of individual structures using genetic operators such as selection, mutation, and reproduction. The operators used in evolutionary computation, is only a simplistic subset of biological processes. Nevertheless, these are sufficiently complex to provide robust and powerful adaptive search mechanisms. The fitness of each individual in the environment effects it capabilities of surviving, or transferring its genes to succeeding generations (see Figure 2).

t:=0;                                           {initialize time}

InitPopulation(P,t);                    {initialize random population of individuals}

EvaluateFitness(P,t);                  {evaluate fitness of all initial individuals in

                                                   the population}

while not terminate(P,t) do        {test for termination criterion, e.g. # of

                                                   generations,satisfactory fitness, etc.}

begin

 t:=t+1;                                       {increase time}

 SelectParents(P,Ps);                  {select subpopulation for reproduction}

 Recombine(Ps);                        {recombine the genes of selected parents}

 Mutate(Ps);                               {mutate (perturb randomly) the mated population}

 EvaluateFitness(Ps,t);                {evaluate new fitness}

 Survive(P,Ps);                           {select the survivors using actual fitnesses}

end;

Figure 2. The basic evolutionary algorithm.

2. Evolutionary Computation models

There are four main evolutionary computation models:

·  Genetic Algorithms,

·  Evolutionary Programming,

·  Evolutionary Strategies,

·  Genetic Programming.

These models differ basically in the way they encode the individuals and application of the genetic operators. These will be discussed in the following subsections.

2.1     Genetic Algorithms

A genetic algorithm(GA) has the following components:

·  a mechanism to encode solutions to problems as strings,

·  a population of solutions represented as strings,

·  a problem dependent fitness function,

·  a selection mechanism,

·  crossover and mutation operators.

The selection mechanism and the other genetic operators are applied in a generational cycles which is basically similar to the algorithm given in Figure 2. Below these are discussed.

2.1.1  Encoding Mechanism

Solutions to the optimization problem are represented as strings. This is accomplished through the use of an encoding mechanism which is problem dependent. Generally, the resultant mapping is a fixed length binary string. It is possible to represent both discrete and continuous variables. However, in the case of real valued variables, the encoding is a two stage process. First, the real variable is mapped linearly to an integer defined in a specified range, then this integer is encoded using a fixed number of binary bits. The binary codes of all variables are then concatenated to obtain a binary string.

Although, in most of the applications integers are directly converted using their respective binary representations, some researchers prefer gray coding. A Gray code [7] represents each number in the sequence of integers {0, ... , 2^N-1} as a binary string of length N in an order such that adjacent integers have Gray code representations that differ in only one bit position. Proceeding through the integer sequence therefore requires changýng only one bit at a time. This defining property of Gray codes is sometimes called the "adjacency property" [2]. For example, the binary coding of {0, ..., 7} (N = 3)  is {000, 001, 010,  011, 100, 101, 110, 111}, while one Gray coding is {000,  001,  011,  010, 110, 111, 101, 100}.  In essence, a Gray code takes a binary sequence and shuffles  it  to  form  some  new  sequence  with  the  adjacency property. There exist,  therefore,  multiple  Gray  codings  for  any given N. A Gray code representation generally improves a mutation operator's (see subsection 2.1.5) chances of making incremental improvements. In a binary-coded string of length N, a single mutation in the most significant bit alters the number by 2^N-1. In a Gray-coded string, fewer mutations lead to a change this large. The disadvantage of using Gray coding is that fewer mutations lead to much larger (generally undesirable) changes. In the Gray code illustrated above, for example, a single mutation of the left-most bit changes a zero to a seven and vice-versa, while the largest change a single mutation can make to a corresponding binary-coded individual is always four. Nevertheless, even this property may be useful, for it may initiate the exploration of an entirely new region in the space of chromosomes.

2.1.2  Fitness Function

Each string is evaluated by using the normalized form of the objective function to be optimized. This fitness function has values in the range [0, 1] which are the fitness of the individuals in the population.  Using the fitness of the string the selection mechanism (see subsection 2.1.3) evaluates them.

2.1.3  Selection

Selection is based on the survival of the fittest mechanism of nature. Individuals which are more fit in some sense defined by the problem survive whereas weaker ones perish. This operator has several different implementations. A fitter individual is allowed to have a higher number of offspring leading to an increased probability of surviving in the subsequent generations. In the proportionate selection scheme, a string with fitness value f_s  is allocated f_s/f_a  offspring, where f_a is the average fitness value of the population. Consequently, strings with fitness greater than the average is allocated more than one offspring. The efficiency of proportionate selection scheme has been improved by the introduction of stochastic remainder technique and the stochastic universal sampling technique. These techniques reduce sampling errors.  Other implementations use a model in which certain randomly selected individuals in a subgroup compete and the fittest is selected. This is called tournament selection scheme. Selection mechanisms such as rank based selection, elitist strategies, and steady-state selection have also been proposed as alternatives to proportionate selection.

2.1.4  Crossover

In nature, the encoding of genetic information admits asexual reproduction (such as by budding). This process typically results in offspring that are genetically identical to the parent, whereas sexual reproduction allows the creation of genetically radically different offspring that are still of the same species.

At the molecular level what simply occurs is that a pair of chromosomes come together, exchange pieces of genetic information and then drift apart. This is called the recombination operation, which referred to as crossover in the EA literature because of the way that genetic material crosses over from one chromosome to another.

Crossover is generally implemented as follows. Pairs of strings are picked at random from the population to be subjected to crossover. Single point crossover is the simplest approach. Here, if the length of the strings is , then a crossover point which can have values in the range 1 to -1 is randomly chosen. The fragments of the two strings beyond this crossover point are exchanged to form two new strings if a randomly generated number is greater than p_c, the crossover rate which is a parameter of the GA.

Crossover mechanisms such as two-point, multi-point, and uniform have been proposed as improvements to the single-point crossover technique.

In the two point crossover scheme, two crossover points are randomly chosen and segments of the strings between them are exchanged. Two point crossover eliminates the single point bias toward bits at the ends of the strings.

Multi-point crossover is an extension of the two-point scheme. Each strings is treated as a ring of bits divided by k crossover points into k segments. One set of alternate segments is exchanged between the pair of strings to be crossed.

Uniform crossover exchanges bits of a string rather than segments. The bits are probabilistically exchanged with some fixed probability. The exchange of bits at one string position is independent of the exchange at other positions.

2.1.5  Mutation

Mutation of a bit is carried out by changing a 0 to 1 or vice versa. Similar to p_c which controls the probability of crossover, another parameter, p_m the mutation rate gives the probability that a bit will be altered. The mutation of a bit does not affect the probability of mutation of other bits.

2.1.6  Generational Cycle

The generational cycle consists of repeated application of selection and the genetic operators to the population. Typically a population size of 30 to 200 is used. Crossover rates are chosen in the interval [0.5, 1.0] whereas mutation rates in the interval [0.001, 0.05]. These parameters are called the control parameters of the GA and are specified before the execution starts.

The generational cycle is terminated  using a stopping criterion such as:

·  reaching a fixed number of iterations,

·  evolving a string with a high fitness value,

·  creation of a certain degree of homogeneity within the population.

2.1.7  Variations of Genetic Algorithms

Recently, there has been considerable research to improve GA performance.

There are some adaptive implementations where the control parameters and encoding are dynamically varied. These are based on the following observation. Although the initial parameter settings may be optimal in the earlier stages of the search, they generally tend to become inefficient during the later stages. Also encodings become too coarse as the search progresses. Generally, two strategies are used. In one strategy, the mutation rate is exponentially decreased as the number of generations increase. This decreases the search rate, and the strings with high fitness are not disrupted as the search converges. In the other strategy, the rate at which genetic operators are applied is dynamically modified based on their performance. Here, each operator is evaluated for the fitness values of strings it generates in subsequent generations.

The search strategy of GAs is inherently parallel. Distributed GAs and parallel GAs have been proposed to take advantage of this fact. Distributed GAs distribute a large population into several smaller subpopulations that evolve independently. The advantages of this approach is two fold: a larger population is explored, and the convergence rates of the subpopulations are also high. Global competition is achieved by exchanging the best strings of the subpopulations. Parallel GAs enable execution of the sequential GA on parallel computers. However, this implementation is not straightforward, the parallelism requires several modifications on the GA structure.

2.2     Evolutionary Programming

Evolutionary  programming (EP) [8] is  a  stochastic  optimization   strategy similar   to  genetic  algorithms,  but  here  both genome like  representations  and crossover  operator is not used. Like  GA,  the EP technique is useful for optimization problems when other  techniques  like  gradient  descent  or direct,  analytical  discovery  fail.  Combinatorial and real-valued function optimization in which the  optimization  surface possesses many locally optimal solutions, are well-suited for the EP technique.

2.2.1  Representation

As mentioned in the previous section, the typical GA approach involves encoding the problem solutions as a binary string.  In the EP approach,  however, the representation follows from the problem. For example, a neural network can be represented in the same manner as it is implemented since the mutation operation does not demand a linear encoding.

2.2.2  Mutation Operator

The mutation operation simply changes aspects of the solution according to a statistical distribution which weights minor variations in offspring as highly probable and substantial variations as increasingly unlikely as the global optimum is approached. There  is a certain tautology here: if the global optimum is not already  known, how can the spread of the mutation operation be damped as the solutions approach it? Several techniques have been proposed and  implemented which address this difficulty, the most widely studied  being the "Meta-Evolutionary" technique in  which the variance of the mutation distribution is subject to  mutation by a fixed variance mutation operator and evolves along with  the solution.

2.3     Evolutionary Strategies

Evolution strategies (ES) [2] were invented to solve technical optimization problems like e.g. constructing an optimal flashing nozzle, and until recently ES were mainly used in the civil engineering discipline, as an alternative to standard solutions. Usually no closed form analytical objective function is available for such problems hence, no applicable optimization method exists, but the engineer's intuition.

In a two-membered or (1+1) ES, one parent generates one offspring per generation by applying normally distributed mutations, i.e. smaller steps occur more likely than big ones, until a child performs better than its ancestor and takes its place. Because of this simple structure, theoretical results for  stepsize control and convergence velocity could be derived. the ratio  between successful and all mutations should come to 1/5: the so-called 1/5 success rule was discovered. This first algorithm, using  mutation only, has then been enhanced to a (+1) strategy which incorporated crossover due to several, i.e. parents being  available. The mutation scheme and the exogenous stepsize control  were taken across unchanged from (1+1) ES. Schwefel later [9] generalized these strategies to the multi-membered ES now denoted by (+) and (, ) which imitate the following basic principles of organic evolution: a population, leading to the possibility of crossover with random mating, mutation and selection. These strategies are termed plus strategy and comma strategy, respectively: in the plus case, the parental generation is taken into account during selection, while in the comma case only the offspring undergoes selection, and the parents die off. denotes the population size, and, denotes the number of offspring generated per generation.

2.3.1  Representation

A single individual of the ES population consists of the following genotype representing a point in the search space. Object variables: Real-valued x_i have to be tuned by crossover and mutation such that an objective function reaches its global optimum. Strategy variables: Real-valued _i or mean stepsizes determine the mutability of the x_i. They represent the standard deviation of a (0, _i) gaussian distribution being added to each x_i as an undirected mutation. With an "expectancy value" of 0 the parents will produce offspring similar to themselves on the average. In order to make a doubling and a halving of a stepsize equally probable, the _i mutate log-normally, distributed from generation to generation. These stepsizes hide the internal model the population has made of its environment, i.e. a self-adaptation of the stepsizes has replaced the exogenous control of the (1+1) ES.

This concept is successful because selection sooner or later prefers those individuals having built a good model of the objective function, thus producing better offspring. Hence, learning takes place on two levels: (1) at the genotype, i.e. the object and strategy variable level and (2) at the phenotype level, i.e. the fitness level.

2.3.2  Selection

Depending on an individual's x_i, the resulting objective function value f(x), where x denotes the vector of objective variables, serves as the phenotype (fitness) in the selection step. In a plus strategy, the best of all (+) individuals become the parents of the next generation. Using comma variant, selection takes place only among the offspring. The second scheme is more realistic and therefore more successful, since no individual may survive forever, which could at least theoretically occur if the plus variant is used. A comma strategy allowing intermediate deterioration performs better, which is not typical for conventional optimization algorithms. Only by forgetting highly fit individuals can a permanent adaptation of the stepsizes take place and avoid long stagnation phases due to misadapted _is. This means that these individuals have built an internal model that is no longer appropriate for further progress, and thus   should better be discarded.

By choosing a certain ratio /, one can determine the convergence property of the ES: If one wants fast, but local convergence, one should choose a small hard selection, ratio, e.g. (5,100), but looking for the global optimum, one should favor a softer selection (15,100).

2.3.3  Basis of Self Adaptation in ES

The following are the basis of self adaptation in ES [10].

·  Randomness: Mutation can not be modeled as a purely random process which would mean that a child is completely independent of its parents.

·  Population size: The population has to be sufficiently large. Not only the current best should be allowed to reproduce, but also a set of good individuals.

·  Cooperation: In order to exploit the effects of a population ( > 1), the individuals should recombine their knowledge with that of others (cooperate) because one cannot expect the knowledge to accumulate in the best individual only.

·  Deterioration: In order to allow better internal models (stepsizes) to provide better progress in the future, one should accept deterioration from one generation to the next. A limited life-span in nature is not a sign of failure, but an important means of preventing a species from freezing genetically.

2.4    Genetic Programming

Genetic programming (GP) is the extension of the genetic model of learning into the space of programs [11]. That is, the objects that constitute the population are not fixed-length character strings that encode possible solutions to the problem at hand, they are programs that, when executed, "are" the candidate solutions to the problem.

2.4.1   Representation

The structures that are being adapted in GP are hierarchically structured computer programs whose size, shape, and complexity can dynamically change during the process. The set of such structures is the set of all possible composition of functions that can be composed recursively from the available set of n functions F={f₁, f₂, ..., f_n} and the available set of m terminals T={a₁, a₂, ..., a_n}. Depending on the problem at hand, the functions may be basic arithmetic operations, Boolean operations or even iterative operators such as Do-Until, etc.

Although, almost all high level programming languages are suitable for expressing and evaluating the compositions of functions described above, initially LISP was chosen for implementation. Recently, there were implementations in C and C++.

The search space for GP is the hyperspace of valid LISP expressions that can be recursively created by composition of the available functions and terminals.

Initial random population is generated by selecting one of the functions from the set F at random to be the root of the tree. Whenever a point is labeled with a function which has k arguments, then k children are created randomly. If a child is a terminal, then the process is complete for that portion of the tree. If the child is a function, then the process continues.

2.4.2  Fitness Function

The raw fitness of any LISP S-expression is defined to be the sum of distances between the point in the range space returned by the S-expression for a given set of arguments and the correct point in the range space. Raw fitness is scaled to produce an adjusted fitness measure.

2.4.3  Fitness Proportionate Reproduction Operator

The reproduction operator for GP is based on the survival of the fittest principle. It is asexual., ý.e., one parent produces one offspring. Each individual has a probability of reproduction proportional to its fitness.

During reproduction, parents remain in the population, therefore it possible that they may repeatedly reproduce.

2.4.4  Crossover

Parents are chosen from the population with a probability equal to their respective normalized fitness values. The operation begins by randomly and independently selecting one point in each parent using a probability distribution. Generally, the number of points in the two parents are not equal. The crossover fragment for a particular parent is the rooted sub tree whose root is the crossover point for the parent. The first offspring is produced by deleting the crossover fragment of the first parent from the first parent and then impregnating the crossover fragment of the second parent at the crossover point of the first parent. The second offspring is produced in a symmetric manner.

3.  Applications of Evalutionary Algorithms

EAs should be used when there is no other known problem solving strategy, and the problem domain is NP-complete. That's where EAs come into play: heuristically finding solutions where all else fails.

Some of the EA applications are listed below:

·  Time-tabling: This has been addressed quite successfully with GAs. A very common  example of this kind of problem is the time-tabling of exams or  classes in Universities, etc. At the Department of Artificial  Intelligence, University of Edinburgh, time-tabling the MSc exams is  now done using a GA [12].

·  Job-shop scheduling:  The Job-Shop Scheduling Problem is a very difficult NP-complete problem which, so far, seems best addressed by branch and bound search techniques. GA researchers, however, are  continuing to make progress on it [12].

·  Game playing:  GAs can be used to evolve behaviors for playing games. Work in  evolutionary game theory typically surrounds the evolution of a  population of players who meet randomly to play a game in which they  each must adopt one of a limited number of moves [12].

·  Computer Aided Design (CAD): General Electric developed EnGENEous a CAD tool. It is a hybrid system, combining numerical optimization tools, expert systems and genetic algorithms [4].

·  Face Recognition: Faceprints was developed by New Mexico State University. It helps to draw a suspect’s face from a witness’s description. The GA generates 20 faces on a computer screen. The witness provides the fitness function by assigning scores to faces on the screen on a 10-point scale. Using this information together with the usual genetic operators additional faces are generated [4].

·  Financial Time-Series Prediction: Prediction Company, has developed a set of time-series prediction and trading tools for currency trading tools for currency trading in which GA constitute an important part [4].

References

1. J. H. Holland, Adaptation in Natural and Artificial Systems, The University of Michigan Press, Ann Arbor, 1975.

2. I. Rechenberg, Evolutionsstrategie: Optimierung technischer Systeme nach Prinzipien der biologischen Evolution, Fromman-Holzboog Verlag, Stuttgart, 1973.

3. D. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning, Addison-Wesley, Reading, MA, 1989.

4. D. Goldberg, “Genetic and Evolutionary Algorithms Come of Age,” Communications of the ACM, Vol.37, No.3, pp.113-119, March 1994.

5. M. Srinivas and L. M. Patnaik, “Genetic Algorithms: A Survey,” IEEE Computer, pp.17-26, June 1994.

6. J. L. Ribeiro Filho, P. C. Treleaven, and C. Alippi, “Genetic-Algorithm Programming Environments,” IEEE Computer, pp.28-43, June 1994.

7. F. Gray, "Pulse Code Communication", U. S. Patent 2 632 058, March 17, 1953.

8. I. J. Fogel, A. J. Owens, and M. J. Walsh,  Artificial  Intelligence Through Simulated Evolution, John Wiley and Sons, NY, 1966.

9. H.-P. Schwefel, Numerische Optimierung von Computermodellen mittels der Evolutionsstrategie, Basel Birkhaeuser, 1977.

10. H.-P.Schwefel, "Collective Phaenomena in Evolutionary Systems", in Proceedings of 31st Annual Meeting of the International Society for General System Research, Budapest, 1025-1033, 1987.

11. J. R. Koza, Genetic Programming: A Paradigm for Genetically Breeding Populations of Computer Programs to Solve Problems, STAN-CS-90-1314, Stanford University, 1990.

12. J. Heitkoetter, and D. Beasley, eds. “The Hitch-Hiker’s Guide to Evolutionary Computation:A list of Frequently Asked Questions  (FAQ)",USENET : comp.ai.genetic. Available via anonymous FTP from rtfm.mit.edu:/pub/usenet/news.answers/ai-faq/genetic/,  1994.

contents                                     home