Hints
from Life to AI, edited by Ugur HALICI, METU, 1994 ã
the neuron as a computational unit
Marifi Güler
Department of Computer Engineering
Middle East Technical University
06531 Ankara, Turkey
The neuron is reviewed from the computational point of view. Fundamentals of the biological neuron relevant to the artificial neuron modelling is briefly discussed. The formal neuron and higher order neuron is revised
1. Neurobiological hints
Neurons are the basic nervous elements and are differentiated into a cell body, or soma, and processes
(projections) extending out from the soma (Fig. 1). The soma is the center of
the cell, containing the nucleus, and it has structures that manufacture
protein, much of which is shipped down the axon by a complex system of axonal
transport. Processes are usually distinguished as axons or dendrites, but not
all neurons have both. Axons are the principal output apparatus, and dendrites
principally receive and integrate signals. Synapses are the points of
communication between neurons, where processes make quasi-permanent junctions
with the soma or processes of another neuron, and they appear to be highly
specialized.
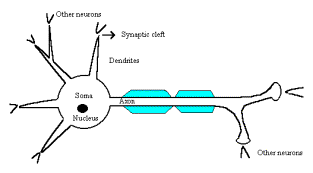
Figure.1 Schematic Neuron.
The central elements in the operation of a neuron are fourfold: (1)
ions in the extracellular and intracellular fluid, (2) a voltage difference
across the cell membrane, (3) single ion channels distributed about the membrane that are specialized to control
cross-membrane passage of distinct ion types, and (4) voltage-sensitive changes
in single ion channels that transiently open the gates in the channels to
permit ions to cross the cell membrane.
There are two general classes
of ions: large negatively charged organic ions concentrated inside the cell and
inorganic ions with systematically changeable concentration profiles inside and
outside the cell. The large organic ions inside the cell cannot pass through
the membrane, and their net charge is negative. Consequently, this affects the
distribution of ions to which the membrane is permeable, since positively
charged ions will tend to congregate inside the cell to balance the negative
charge.
The inorganic ions that play the role are potassium (K+),
sodium (Na+), calcium (Ca++), and chloride (Cl-).
When the cell is at rest (that is, unless the membrane is stimulated), the Na+
and Ca++ channels block the passage of Na+ and Ca++
. Thus, K+ concentrates inside the cell, and Na+
and Ca++ concentrate
outside. The concentration forces counteract the electric forces leading the
concentration of negative charges along the inside of the membrane and positive
charges along the outside. This yields an electric potential across the
membrane about -70 millivolts (mv).
This potential is called the resting potential.
When the cell is stimulated, for example by an electric current or by a
particular chemical, there is a change in membrane's resting potential. The
change in resting potential induced by an incoming signal at the synapse is the
synaptic potential.
Depending on the synaptic events, the postsynaptic response to the
synaptic potential may be a decrease, for example from -70 mv to -60 mv, or an
increase, for example from -70 mv to -80 mv, in the membrane potential Em.
These effects on Em are referred to as depolarization and
hyperpolarization respectively.
A cell may receive thousands of signals via its presynaptic connections
during a millisecond. Signals interact as currents sum to create a larger depolarization;
or, if the effects were hyperpolarizing, to prevent depolarization; or, if the
effects are opposite, to interfere and cancel. If, after the integration of
depolarizing and hyperpolarizing potentials, there is sufficient current to
depolarize the membrane by a certain critical amount known as the firing level
(about 10 mv), then the cell produces a large and dramatic output. This
transient jump in potential is called an action potential or a spike due to its
shape, and the neuron is said to be firing.
Depolarizing synaptic potentials are called excitatory postsynaptic
potentials (EPSPs) because they contribute to the generation of an action
potential by bringing Em closer to the firing level. Conversely,
hyperpolarizing synaptic potentials tend to diminish the probability of the
generation of an action potential, they are called inhibitory postsynaptic
potentials (IPSPs).
When the membrane is polarized above its firing level, the Na+
channels cease briefly to gate Na+, thereby permitting Na+
to rush into the cell. This results in depolarization of the membrane further,
which then induces changes in yet more Na+ channels to allow further
Na+ influx. Thus, a self-generating, explosive effect is produced.
The mean channel open time is only 0.7 msec, and, therefore, as Em
reverses from, say, -70 mv to +55 mv, Na+ conductance is suddenly
inactivated, and K+ begins to move out of the cell, which initiates
the restoration of the resting
potential. This activity of ions results in the generation of an action
potential or a spike (Fig. 2).
After the generation of a spike, some time must elapse before the
neuron to be able to fire again; this is called its refractory period. During
this period, the neuron transports the ions in the opposite direction, pumps Na+ out of the cell and K+ is drawn
in, in order to achieve the original distribution. This requires a supply of
energy provided by the cellular metabolism. A special protein called carrier
uses the metabolic energy provided by the ATP (adenosine triphosphate) to pump
the Na+ and K+ back to their original sites.
The conductances and dynamics of Na+ and K+ are
described by the Hodgkin-Huxley equations (1952). The dynamic system defined by
those equations is a complex system, difficult to analyze. It exhibits very
interesting phenomena such as chaos, transitions, bifurcation etc,. The study
of the Hodgkin-Huxley equations is an ongoing activity of research.
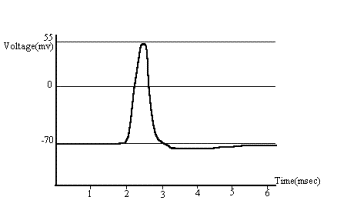
Figure 2 The action potential.
There are two fundamental types of connection between neurons:
electrical synapses and chemical synapses. Electrical synapses are of two
types: (1) those generating field potentials, in which sending and receiving
neurons are so closely positioned that current flow in one induces field
changes in its neighbour, and (2) gap junctions, which consist of thin protein
tubes connecting the axon of one neuron to the dendrite or axon of another. The
tubes are so narrow as to permit the transfer of only very small ions such as
Na+ and K+, and it is via the transfer of these ions that
signals are transmitted from one neuron to the next. Electrical synapses are
mostly found in primitive nervous systems, whereas chemical synapses are more
common in the mammalian nervous system. Electrical synapses are believed to
have a special functional significance.
Electrically coupled cells can fire synchronously, which is not true for
chemically coupled cells because of the synaptic delay that occurs in chemical
synapses.
In chemical synapses, it is Ca++ ions and Ca++
channels that play the crucial role. When a spike reaches to the end of the
presynaptic axon, it opens voltage-sensitive Ca++ channels. Ca++
rushes into the cell which, in turn, augments the amount of available metabolic
energy. This energy is used to move the vesicles of neurotransmitters toward
the membrane. Neurotransmitters, or simply transmitters, are molecules used to
transmit the message about the spike from the presynaptic to the postsynaptic
cell.
The transported vesicle fuses with the membrane and releases
transmitters into the synaptic cleft (Fig. 3). The transmitters diffuses toward
the postsynaptic cell and binds to its membrane at some specialized sites
called receptors. The coupling of the transmitter to the receptor activates
some postsynaptic molecules, here called actuators. The actuators exert an
action over both the presynaptic and postsynaptic neurons, as well as
neighbouring cells. The whole procedure causes a time delay, known as the
synaptic delay, between the arrival of the presynaptic spike and the activation
of the actuators.
Depending on the type of transmitter released and on the character of
the receptor sites, an EPSP or an IPSP is produced. The process of interfusion
and integration of currents then begins in the receiving cell, as described
earlier.
There are various types of neurotransmitters and the use of different
transmitters produced by the same neuron is dependent on the level of activity
at the axon. Low spiking activity may be associated with the use of a certain
type of transmitter, whereas high spike
firing may release the other type. In this way, different postsynaptic cells
are activated if the presynaptic
spiking changes.
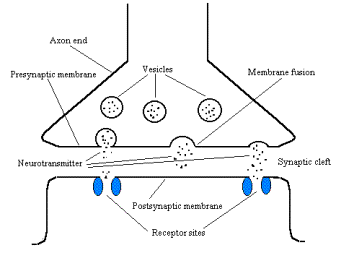
Figure 3 Schematic diagram showing the release of
neurotransmitters.
It is not only the neurotransmitters that play role in exchanging
chemical information between synapses. Those other chemicals, which we call
modulators here, affect the amount and type of transmitter released from the
presynaptic neuron and/or sensitivity of the receptors to certain type(s) of
transmitters. The activity in one neuron can act upon other neurons in the
neighborhood via the modulators.
Experiential input changes the neurotransmitter signals that neurons
send, changes number of synapses, changes the structure of neurons. The
exchange of chemical information between different synapses accounts for both
synaptic cooperation and competition. In the first case, the development of one
synapse facilitates the growth of the contact with another source of
information, providing the basis for associative learning. In the second case,
the development of one synapse inhibits
the growth of another pathway. This establishes a mechanism of competition
between different paths for the control of the postsynaptic cell.
Neurobiology of the neuron is a very broad subject; the interested
reader is referred to the literature (e.g. Shepherd, 1988; Black, 1991).
2. Learning
The fundamental cognitive task performed by neural networks (biological
or artificial) is learning. Learning can be described as the procedure of
adjusting the structural entropy of the network to the entropy of the
environment (external input) in order to model the environment.
It is important to note that learning should not be confused with
memorizing. Learning enables the neural system to fulfill some defined purpose
which may be simple survival or a complex subject like pleasure, science, arts
etc,. This aspect of learning is referred to as the generalization in artificial
neural networks.
After being trained on a number of examples of a relation, the network
should be able to induce a complete relationship that interpolates and
extrapolates from the examples in a sensible way. Although traditional methods
of AI can readily solve these tasks if the generalization rules are known, e.g.
in the case of expert systems, they have difficulty in establishing such rules
on their own. There are several ways to quantify generalization and developing
a theoretical framework for the generalization is an active research topic.
During learning, some synaptic connections are strenghtened and/or some
new connections are created while some other
connections are weakened or completely disabled in order to represent
the regularities within the received data. Learning is not a simple copying
process; repeated observation of the same facts is often necessary so that the
regularities can be discovered. Learning in biological systems is a complex
process depending on the mutual interaction of action potentials, transmitters,
receptors, modulators, proteins, DNA, etc,.
The amount and type of transmitters and receptors determine the
strength of a synapse. The oldest and most famous of all learning rules, known
as the Hebb rule, is often used to describe the synaptic plasticity. Hebb rule
was made in a neurobiological context, however, it does not require the
knowledge of any electrical or chemical details of the synapse. We may expand
and rephrase it as a two-part rule as follows:
1. If two neurons on either side of a synapse
(connection) are activated simultaneously (i.e. synchronously), then the
strength of that synapse is selectively increased.
2. If two neurons on either side of a synapse are
activated asynchronously, then that synapse is selectively weakened.
Thus, a Hebbian synapse uses a time-dependent, highly local, and
strongly interactive mechanism to increase synaptic efficiency as a function of
the correlation between the presynaptic and postsynaptic activities.
In artificial neural networks, a parameter, called synaptic weight, is
associated to the synapse to denote its strength. Hebb rule, or various forms
of it derived from the minimization of a cost function, is almost always used
to develop a learning algorithm.
3. The formal neuron
The neuron model commonly used in artificial neural networks is the
McCulloch-Pitts type and referred to as the formal neuron (Fig. 4). The neuron
computes a linear weighted sum over the external inputs (or over the outputs
from the other neurons) x1, x2,...xN,
and also accounts for a threshold (firing level) . The resulting sum is
applied to a nonlinear activation function f
to obtain the output y:
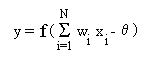 (1)
(1)
The hard limiter is often taken as the activation
function. Accordingly, the neuron produces an output +1 if the hard limiter
input is positive, and -1 if it is negative.
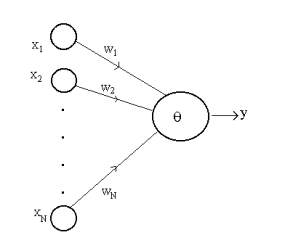
Figure 4 The formal neuron.
Using the Hebb rule for training the neuron in case of supervised
learning leads to the following update of the weights:
![]() k =
1, . . . , N (2)
k =
1, . . . , N (2)
where wk(p) is the amount of change in wk induced by the presentation of the pattern
p and xk(p) is the component of the pattern corresponding to
the kth channel.
d(p) denotes the target or desired
output for the pattern p. is a positive constant that
determines the rate of learning.
If the update rule is applied only for the patterns that are not
classified correctly using the current weight values, while no update is
applied for the patterns that are already learned, the Widrow-Hoff rule is
concluded;
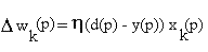 k = 1, . .
. , N (3)
k = 1, . .
. , N (3)
The neuron using the above rule will learn the training patterns
provided the patterns are drawn from two linearly separable classes.
Multilayer of formal neurons, called the multilayer perceptron, is used
in practice. The role of the hidden neurons in the multilayer perceptron is to
enable learning of the patterns that are not linearly separable. The multilayer
perceptron has been applied to solve some diverse problems by training it with
the highly popular backpropagation learning algorithm. The backpropagation algorithm is a gradient-descent based
algorithm and extends the Widrow-Hoff rule for the hidden neurons.
In case of unsupervised learning, where there are no target outputs,
the Hebb rule follows as;
![]() k = 1, . . .
, N (4)
k = 1, . . .
, N (4)
This strengthens the output for each input presented, so frequent input
patterns will have most influence in the long run, and will come to produce the
largest output. Eqn.(4) has been modified in various forms leading to detection
of the principal components, and formation of the feature maps.
The reader is referred to the literature for a comprehensive study of
the points discussed in this section, and for an introduction to the
fundamentals of the artificial neural networks (e.g. Hertz et. al., 1991).
4. Higher-order neurons
The threshold mechanism of the formal neuron is not the only
nonlinearity that plays an important role in information processing in the
brain. Over the years, a substantial body of
evidence has grown to support the presence of nonlinear synaptic
connections and multiplicative-like operations. This is not an unexpected
result considering the sophistication of the chemical processing at the
synapse. We refer the reader to the review article by Koch and Poggio (1992)
for details.
The neural units that have multiplicative synapses are called
higher-order neurons (HONs). A HON is usually studied for bipolar (+1 or -1)
inputs and output. A HON for N = 2 input dimensions is shown in Fig. 5. The
output y is computed in accordance
with
![]() (5)
(5)
where sgn denotes the hard
limiter or sign function. The neuron can learn the XOR problem using the
higher-order synapse which causes a polarization as w12x1x2.
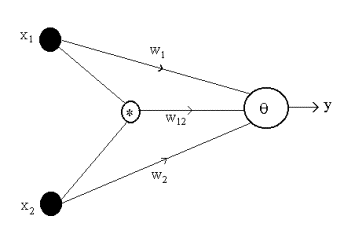
Figure 5. Higher-order neuron for N = 2.
HONs are capable of learning any problem, whether linearly separable or
not, in any N dimensions. The ability to capture higher-order correlations
within the training data is, however, rendered by the combinatorial increase of
the number of weights in the dimensionality of the inputs; there are 2N-1
weights in total. If it is known a priori that the problem to be implemented
possesses a given set of invariances like in the translation, rotation and
scale invariant pattern recognition problems, those invariances can be encoded,
thus eliminating all the synapses which are incompatible with the invariances
(Giles and Maxwell, 1987; Spirkovska and Reid, 1993). This is, however, not a
generic approach since the invariances most often are not known in advance and
usually are very complicated.
Recently, it was suggested that selection of the relevant higher-order
synapses, with no priori knowledge assumed, may be possible, and those relevant
synapses may be concluded dynamically without a need to compute all the weights
explicitly (Güler and Þahin, 1994). The authors are actually able to
propose an algorithm for the selection of the relevant higher-order synapses as
stated above, in a study in preparation for publication.
References
1. Black, I.B.(1991) Information
in the brain. The MIT Press.
2. Giles, C.L. and Maxwell,
T.(1987) Learning, invariances, and
generalization in higher-order neural
networks. Applied Optics 26
p. 4972-4978.
3. Güler, M. and Þahin,
E.(1994) A binary-input supervised
neural unit that forms input dependent higher-order synaptic correlations. Proc. of
World Congress on Neural Networks, III, p. 730-735.
4. Hertz, J., Krogh, A. and
Palmer, R.G.(1991) Introduction to the Theory of Neural
Computation. Addison-Wesley.
5. Hodgkin, A.A. and Huxley,
A.F.(1952) A quantitative description
of membrane currents and its application to conduction and excitation in nerve.
J. Physiology 117 p. 500.
6. Koch, C. and Poggio,
T.(1992) Multiplying with synapses and
neurons. In: McKenna, T., Davis J.,and Zornetzer F.S. (Eds.) Single Neuron Computation p. 315-345.
7. Shepherd, G.M.(1988) Neurobiology.
Oxford University Press, New York.
8.
Spirkovska,
L. and Reid, M.B.(1993) Coarse-coded
higher-order neural networks for PSRI object recognition. IEEE Trans. on Neural Networks 4 p. 276-283