 |
|
Q1
a) Explain briefly the structure of Boltzmann
machine. |
|
b)
Explain what is energy function. |
|
c)
How Bolzmann machine is used for optimization
problems? |
|
d)
Explain cooling schedule? Explain briefly
|
|
e)
Why the temperature in a Boltzmann Machine should be
decreased very slowly when it is used for optimization. |
|
f)
What are the advantages and disadvantages of using Boltzmann
machine for optimization instead of Hopfield
Network? |
|
Q2)
Consider a Boltzmann machine having N neurons. Call
neuron i and j as adjacent
iff
i=j+1, or i=j-1 or (i=1 and j=N) or (j=1 and i=N).
Let
the connection weights are as follows
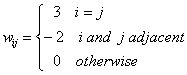
|
|
a)
Draw the Boltzman machine for N=6 by showing
the nonzero connections and their weihgts. |
|
b)
Let N=6 and temperature T>0. If x(k)=[1,0,1,0,1,0]T,
what are the possible next states, i.e. x(k+1) |
|
c)
For x(k)=[1,0,1,0,1,0]T, what is the
energy difference if one of the neurons with output
1 is set to 0 in the next state? |
|
d)
Repeat b, for a neuron with output 0 is set to
1 in the next state. |
|
e)
Does the state [1,0,1,0,1,0]T correspond
to a local minima of the energy function of this Boltzmann
machine. Explain why? |
|
Solution: |
a)
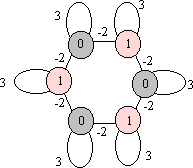
|
|
b)
x(k)=[1
0 1 0 1 0]T
x1(k+1)=[0
0 1 0 1 0]T
x2(k+1)=[1
1 1 0 1 0]T
x3(k+1)=[1
0 0 0 1 0]T
x4(k+1)=[1
0 1 1 1 0]T
x5(k+1)=[1
0 1 0 0 0]T
x6(k+1)=[1
0 1 0 1 1]T
|
|
c)
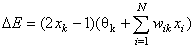
note that
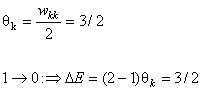
Another
way of solution:
E(k)=-9/2
E(k+1)=-6/2 DE=3/2
|
|
d)
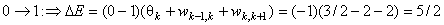
or
E(k)=-9/2,
E(k+1)=-4/2, DE=5/2
|
|
e)
Yes, transition to any neighbouring state causes increase
in the energy, therefore it is a local minima |
|
Q3)
Consider the following Boltzmann machine for which
the state transition probability is given by the formula
1/(1+ exp(-DCk(u)/T)
where
T is the temperature.
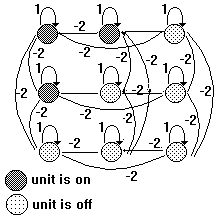
|
|
a)
Describe formally the Cb, Cr, Cc connections, where
Cb is the bias connections, Cr is the inhibitory connections
between the elements of the same row, and Cc is the
inhibitory connections between the elements of the
same column, |
|
b)
If T is finite and greater than 0, which is(are)
the most probable next configuration(s) |
|
c)
If T is 0, which is(are) the possible next configuration(s) |
|
d)
If T is finite and greater than 0, which is(are)
the expected final configurations if temperature is
decreased very smoothly. |
|
Q4)
Given the Boltzmann-Gibbs distribution P(x)=(1/Z)exp(-E(x)/T)
show that P(xj|xj')=1/(1+
exp(DE/T))
where DE=E(xj)-E(xi)
satisfies the equlibrium balance equation which is P(xj|xj')P(xi)=
P(xi|xj)P(xj) |
|
a)
Show that DE(xk|x)=(2xk-1)(Si
wi(k)xi+q
(k)) for the binary state Boltzmann machine whenever
wij=wji, wii=0 |
|
b)
Derive DE(xk|x)
for the binary case. |
|
Q5)
For the binary Boltzmann machine given in the figure,
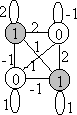
|
|
a)
What is the current state? (index neurons in row major
order) |
|
b)
What are the probable next states if T>0 and what is
the energy difference for each of them. |
|
c)
Which one is the most probable one among those found in
b) |
|
d)
If T is decreased very slowly, which one is the
most probable final state. |
|
Q6)
Consider the Binary output Boltzmann Machine having 2x2
elements for which wki,ki=1 k,i=1,2,
w12,21=w21,12=2, w11,22=
w22,11=-2 and all the other connection weights
are -1. The initial state is:
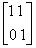
|
|
a)
What are the probable next states if temperature T>0
? |
|
b)
Which one is the most probable state(s) among them ? |
|
c)
What is the most probable final state(s) if the
temperature is gradually decreased to 0 ? |
|
|
 |