Q1) Find out the connection strengths of the Hopfield Network X {0,1}n to minimize the following cost functions

a)

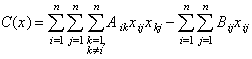b)

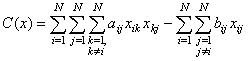c)

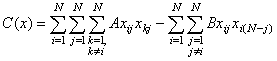d)

Solution:

d)

or

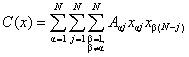Q2) Show how the Hopfield network can be used for solving the independent set problem. Given a graph G={V,E}, the independent set problem is to find one of greatests  subset V' of V, such that for any i,j V', there exit no edge between i and j in G.  For this purpose use  variable Xi such that Xi= 1 if  i V',  and Xi=0 otherwise.

a) given a graph, what should be the structure of the corresponding Hopfield network

b) write the Energy function

c) write the cost function to be minimized and indicate which part stands for the feasibility, and which part is for optimization

d) by comparing the energy and cost functions you defined above, find out the corresponding connection weights and bias currents

Q3) Consider a Hopfield Network having 3x3  elements having output value {-1,1}. For this network we want to have local minima in its energy function  if it represent the letter I, which may be shifted, but not rotated. For this purpose write the energy function and find out the connection strengths. Hint: Try to force no two elements to be on together if  they are in the same row, but support  the elements to be on together if they are in the same column.

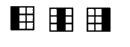
Q4) For the Eight Queen problem, which requires the placement of Eight Queens on a chessboard such that no queen attacks another one.

a)Write a cost function which will have minimum at the solution(s) of the problem (do not attempt to find out the connection strength)

b) Intuitively indicate which connections for a Boltzmann Machine, having 64 nodes  corresponding to the squares of the chessboard, and "on" values indicates that a queen is placed there, should be inhibitory, and which of them should be excitatory

Q5) On a chess board, you are desiring to place as many  queens as possible so that none of them is attacking any other. Write verbally the constraints to be satisfied in this problem and then write a cost function that have a minimum whenever all the constraints are satisfied. Then find out the connection weights for a binary state Hopfield network so that the energy function is order preserving. Discuss the feasibility of your solution by  explaining if every local minimum is a valid solution or not.

Q6) Design a  Binary output Hopfield Network having N=nxn elements such that the energy function has local minima for the states having symmetry with respect to primary diagonal axis, i.e. x_ij=x_ji, i,j=1..n. For this purpose first write a cost function and then find the connection weights.

Q7) If an NxN binary Hopfield network is to be used to minimize the following function, 

 then find out appropriate connection strengths.

Solution:

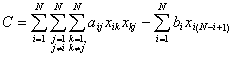
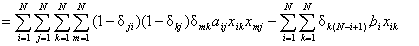
By comparing E and C we obtain

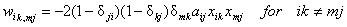
Notice that

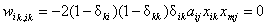
Therefore we have
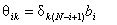