 |
|
|
Q1)
Consider the following orthonormal sets of input patterns,
applied to an interpolative associative memory
u1=[1,0,0,0]T,
u2=[0,1,0,0]T, u3=[0,0,1,0]T
The
respective stored patterns are
y1=[5,1,0]T,
y2=[-2,1,6]T, y3=[-2,4,3]T
|
|
a)
Find out the connection weights for the Linear Associator
|
|
b)
Show that the memory associates perfectly |
|
Q2)
a) What is associative memory? Explain briefly . |
|
b)
What is BAM, explain briefly |
|
c)
If the (x,y) pairs ((1,0,0), (1,0)); ((0,1,0),(1,1));
((0,1,1),(0,1)) are to be stored in a BAM, show the structure
of the BAM and the connection strengths |
|
d)
if x=(0,0,1) is applied at x layer, what is the associated
y in this BAM |
|
Q3)
Consider the following synchronous discrete Hopfield
network
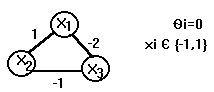
For
each state of the network, indicate if it is a fixed
(equilibrium) point or not. If it is not a fixed point
explain if it is in the basin attraction of some fixed
point or not. |
|
Q4)
We have a hopfield network with states from binary
space x {0,1}N and also examplars
uk {0,1}N k=1..K . |
|
a)
What should be the connection weights and biases to
use this Hopfield network as autoassociative memory.
|
|
b)
Give an energy function for this network and
show that it is convergent |
| Q5)
You will use a bipolar Hopfield autoassociative memory
which will remember memory elements (1,1,1,1)
and (1,1,-1,-1). |
| a)
Find the weight matrix (do not set diagonal terms
to zero) |
|
b)
Test the net using (1,1,1,1) as input |
|
c)
Test the net using (1,1,-1,-1) as input |
|
d)
Test the net using (1,1,1,0) as input |
|
e)
Repeats a-d with the diagonal terms in the weight
matrix set to zero. Discuss any differences you
find in the responds of your net |
Q6)
Hopfield network is to be used as auto-associative memory.
Given the pattern vectors
 |
a)
find corresponding input vectors for hopfield network
with row major ordering, i.e.
x1
x2 x3
x4
x5 x6 |
b)
Draw the corresponding hopfield network. |
c)
If first 2 patterns are used in the training of the network,
then find out the connection weights. |
d)
What will be the final state of the network if the initial
state is the third pattern? |
e) how the number of vectors trained to the system
affects the performance? |
f)
If all of the patterns were used in training the
network, then what would be the connection weights. |
|
Solution: |
|
a) Let
black = 1, white = -1
u1=[-1,
1, -1, 1, -1,-1]T
u2=[-1,
1, -1, -1, 1, -1]T
u3=[-1,
-1, 1, -1, 1, -1]T
|
|
b)
|
|
c)
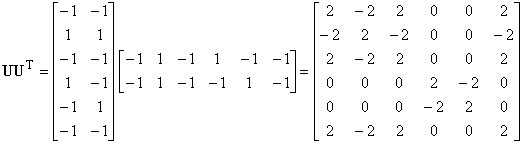
Set
diagonal entries to 0, so

|
|
d)
X(0)=
u3=[-1, -1, 1, -1, 1, -1]T
Assuming
synchronous update



It
is oscillating.
|
|
e)
Since the capacity of the Hopfield network is
limited, spurious states emerge as the number
of samples stored increases, furthermore
some of the stored patterns are no more fixed
states of the network. |
|
f)
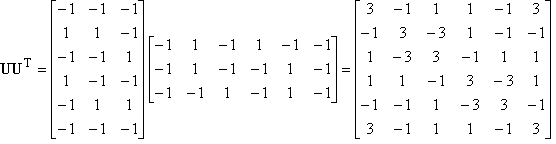
Set
diagonal entries i.e. to 0, so
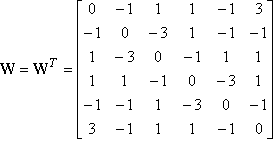
|
|
Q7)
You will use a bipolar Hopfield autoassociative memory
which will remember memory elements
u1=[+1,
+1, -1]T and u2=[+1, -1, -1]T. |
|
a)
Find the weight matrix (do not forget to set diagonal
terms to zero) |
|
b)
All possible states of such a network are given below:
x0=[-1,
-1, -1]T
x1=[-1,
-1, +1]T
x2=[-1,
+1, -1]T
x3=[-1,
+1, +1]T
x4=[+1,
-1, -1]T
x5=[+1,
-1, +1]T
x6=[+1,
+1, -1]T
x7=[+1,
+1, +1]T
Find
the next state for each of them assuming synchronous
update
|
|
c)
Which of the states given in part b are fixed states,
which of them are in basin attraction of other states,
and which of them are oscillatory |
|
d)
Is your network successful in storing u1
and u2 |
|
e)
Is there any spurious fixed state? If yes, which
fixed states are spurious? |
|
f)
If asynchronous update were going to be applied, what
would be the possible next states of the states given
in part b)? Show all possible transitions on the
hypercube given below
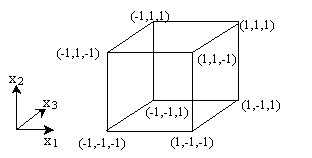
|
|
g,h,i)
repeat c,d,e for asynchronous update |
|
Solution: |
|
a)
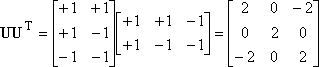
By
setting diagonal entries, i.e. wii to 0
we obtain
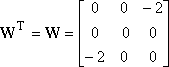
|
|
b)
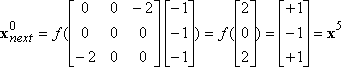
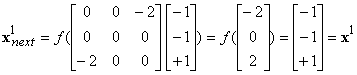
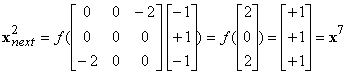
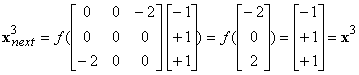
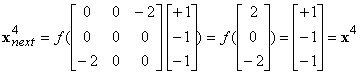

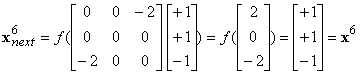
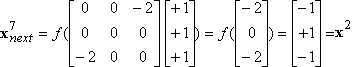
|
|
c)
x1,
x3, x4, x6 are fixed
states,
x0
and x5 are oscillating
x2
and x7 are oscillating
|
|
d)
Since u1=x6 is a fixed state it
is successfully stored as an memory element,
it is the same for u2=x4.
|
|
e) x1
and x3 are spurious fixed states. |
|
f)
Notice that the ith row of
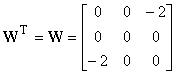
corresponds
to the weight vector of the ith neuron
In
order to find the possible next states of x0=[-1,-1,-1]T
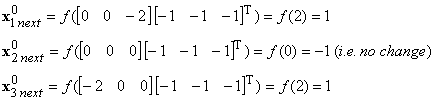
Therefore
the possible next states of x0=[-1,-1,-1]T
can be obtained by changing only the ith
entry for i=1,2,3, which are [+1, -1, -1]T=x4,
[-1, -1, -1]T=x0, [-1, -1, +1]T=x1
The
procedure is the same for the other states
|
|
|
|
i=1 |
i=2 |
i=3 |
|
x0=[-1,
-1, -1]T |
[+1,
-1, -1]T=x4 |
[-1,
-1, -1]T=x0 |
[-1,
-1, +1]T=x1 |
|
x1=[-1,
-1, +1]T |
[-1,
-1, +1]T=x1 |
[-1,
-1, +1]T=x1 |
[-1,
-1, +1]T=x1 |
|
x2=[-1,
+1, -1]T |
[+1,
+1, -1]T=x6 |
[-1,
+1, -1]T=x2 |
[-1,
+1, +1]T=x3 |
|
x3=[-1,
+1, +1]T |
[-1,
+1, +1]T=x3 |
[-1,
+1, +1]T=x3 |
[-1,
+1, +1]T=x3 |
|
x4=[+1,
-1, -1]T |
[+1,
-1, -1]T=x4 |
[+1,
-1, -1]T=x4 |
[+1,
-1, -1]T=x4 |
|
x5=[+1,
-1, +1]T |
[-1,
-1, +1]T=x1 |
[+1,
-1, +1]T=x5 |
[+1,
-1, -1]T=x4 |
|
x6=[+1,
+1, -1]T |
[+1,
+1, -1]T=x6 |
[+1,
+1, -1]T=x6 |
[+1,
+1, -1]T=x6 |
|
x7=[+1,
+1, +1]T |
[-1,
+1, +1]T=x3 |
[+1,
+1, +1]T=x7 |
[+1,
+1, -1]T=x6 |
Possible
transitions are shown on the hypercube below
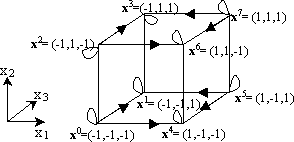
|
|
g)
x1, x3, x4, x6
are fixed states,
x0
is in basin attraction of x1 and
x4
x2
is in basin attraction of x3
and x6
x5
is in basin attraction of x1
and x4
x7
is in basin attraction of x3
and x6
|
|
h)
Since u1=x6 and u2=x4
are again fixed states, they are successfully
stored as an memory elements, |
|
i)
x1 and x3 are spurious fixed states |
|
Q8)
BAM is to be used to remember the following pairs.
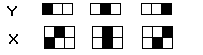
|
|
a)
Draw the corresponding BAM network |
|
b)
write corresponding X and Y vectors with row
major ordering |
|
c)
if these three pairs are used for the training, find
the corresponding connection weights |
|
d)
assume initially the network is converged to the third
pattern, and then the following pattern is
applied at X layer, find out the final configuration
that the network converges
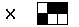
|
|
e)
What is the energy just after the new input pattern
is applied |
|
f)
What is the final energy |
|
Q9)
Consider bipolar Hopfield autoassociative memory used
to store NxN black-white images, in which the weight matrix
is symmetrical and diagonal entries are zero. |
|
a)
Show that the negative of the image (i.e. blacks are converted
to white, and vice versa) is a fixed point whenever the
original is. |
|
b)
Compare the behavior of the network for the cases the
original and the negative of an image is applied as the
initial state (not necessarily a fixed point) |
|
Q10)
Consider
the following sets of input patterns, applied to an interpolative
associative memory
u1=½
[1,-1,-1,-1]T
u2=½
[-1,-1,-1,1]T
u3=½
[-1,-1,1,-1]T
The
respective output patterns are
y1=[1,1,-1]T
y2=[1,1,1]T
y3=[-1,1,1]T
|
|
a)
Show that ui i=1..3 are orthonormal. |
|
b)
Find out the connection weights for the Linear Associator.
|
|
c)
Show that the memory associates perfectly. |
|
d)
If u=½[0.6, -1, -1, -1] T is
applied at the input, what will be the output. |
|
e)
What is the error e at the
input and the error er at the
output for the pattern given in c ? |
|
f) Now BAM is to be used instead of Linear Associator.
If the neurons at the v layer are set to
u=½[0.6, -1, -1, -1] T at t=0,
to which state the network will converge? |
|
|
 |