 |
|
|
Q1)
Explain the analogy between Biological Neuron and Artificial
Neuron |
|
Q2)
Consider
an NxN input grid and a hidden array of (N-2)x(N-2) neurons
with threshold activation function (no neurons correponding
to the borders of the input grid). Any neuron Xij
in this layer has connections from the cell (i,j) and
its 8 neighbours on the input grid (that is, a receptive
field of 3x3 cells around cell (i,j) ). This hidden neuron
array is connected to a single output neuron
Y through two hidden neurons, namely A and B
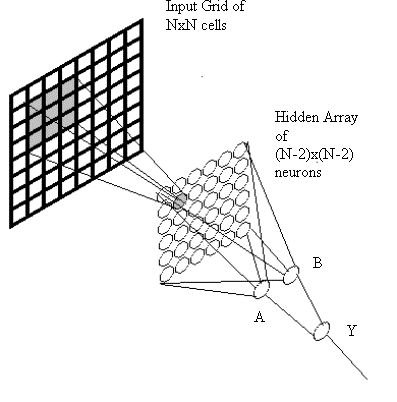
This
network will be used to find out if the following 3x3
pattern is placed somewhere on the input grid or not.

Make
the necessary connections |
|
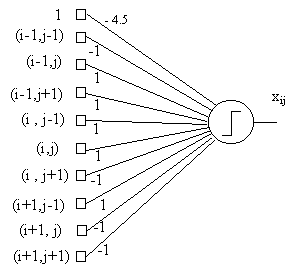
a)
to
the neuron Xij on the hidden array from its
receptive field on the input grid, such that the output
of Xij will be 1 if the above 3x3 pattern is
placed in its receptive field. |
|
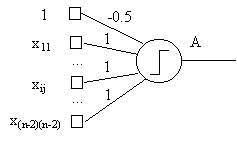
b)
from
the neurons on the hidden array to the neuron A, such
that, the output of
A will be 1 if there is at least one active neuron
in the hidden array of neurons |
|
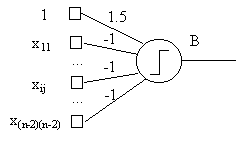
c)
from
the neurons in the hidden array to the neuron B, such
that, the output of
B will be 1 if there is at most one active neuron
in the hidden array of neurons |
|
d)
from
the neurons A, B to
neuron Y, such that exactly one neuron is active
in the hidden array. |
|
Solution |
| Assume
Black=1 and White=0, and indexing of the input grid
starts with (0,0), indexing of xij starts with
(1,1). Use f(a) is the threshold function taking value
0 and 1 |
|
a)
|
|
b)
|
|
c)
|
|
d)
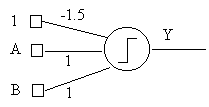
|
Q3)
Design a neural network to detect 3x3 pattern (Black=1,
White=0) given in the figure if it appears anywhere
but exactly once on a 10x10 input grid
|
 |
|
Q4)
You have a 3x3 input board, on which you may have several
input patterns. You want to identify if the pattern is
an I, or C, or T. Therefore you have 9 binary input perceptrons
in the input layer, and you have 3 output units These
outputs will be on only if the corresponding pattern is
placed on the input board. Suppose that you have 3x2+3x2
hidden units, which will check if the the elements in
the corresponding row/column on the input board are all-on/all-off.
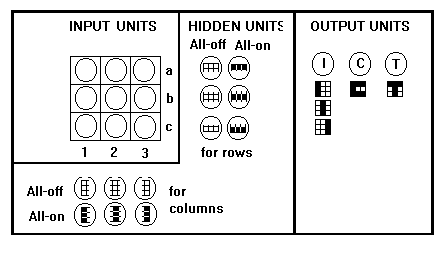
|
|
a)
Show the necessary connections between the input and hidden
units and
find out their
strengths to make those hidden units to work properly |
|
b)
Make necessary connections between the hidden units and
output unit "I" to make this unit to work properly. |
|
c)
Is it possible to make the output unit "C"
to work properly, by constructing connections only only
from the hidden units? If your answer is yes, show how?
If your answer
is no explain why, and show how can you manage it if you
use also connections from the input layer. |
|
d)
repeat part c) for the output unit "T". |
|
Q5)
Consider the following boolean functions
f1=w.x'.y'.z'
and
f2=x'+y+z
Implement
f1 and f2 by using a single perceptron in each having
output characteristic |
|
a)
f(a)=1
if a>=0 and f(a)= 0 otherwise |
|
b)
f(a)=1 if a>=0 and
f(a)= -1 otherwise |
|
Q6)
In binary representation of images, each pixel has value
either 0 or 1. For the enhancement of the images, smoothing
is a process in which the value of a pixel in the smoothed
image is determined by considering its neighborhood in
the original image, such that it is assigned value 1 if
the most of the pixel in this neighborhood has value 1
and assigned value 0 otherwise. Design a neural network
for smoothing 100x100 pixel images by considering the
neigborhood with 8 pixels around (so 9 pixels all togetger).
Clearly indicate the connections and neuron characteristics
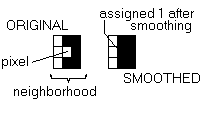
|
|
Q7)
Consider an NxN input grid and an array of NxN output
neurons with threshold activation function. Any output
neuron (i,j) has connections from the cell (i,j) and its
8 neighbours on the input grid (that is, a receptive field
of 3x3 cells around cell (i,j) ) through some hidden neurons.
Suppose
that a KxL, where K,L>3, rectangle pattern is going
to be placed somewhere on the input grid, such that none
of the edges of the rectangle is placed on the borders
of the grid. |
|
a)
i) Show all possible cases on the 3x3 receptive field,
for which the cell (i,j) is on an edge of the rectangle.
ii)
What is the number of cells in this receptive field belonging
to the rectangle? |
|
b)
Repeat a)
for the case cell(i,j) is corresponding to a corner of
the rectangle |
|
c)
If the aim is to have only the 4 neurons on the output
layer corresponding to the corners of the rectangle to
be active, what should be the connection weights and the
threshold values for the hidden and output neurons. (Hint:
2 hidden neurons for each output neuron (i,j) is enough
for this purpose) |
|
Q8) We want to design an expert sytem which makes decisions according to the
rules in its rulebase:
If
(A<a1) then (A is SMALL)
If
(a1£A<a2)
then (A is MEDIUM)
If
(a2£A)
then (A is LARGE)
If
(B<b1) then (B is SMALL)
If
(b1£B)
then (B is LARGE)
If
(A is SMALL)
then (DECISION1)
If
(A is MEDIUM) and
(B is SMALL)
then (DECISION 2)
If
(A is MEDIUM) and
(B is LARGE)
then (DECISION3)
If
(A is
LARGE) and (B
is SMALL) then (DECISION 4)
If
(A is LARGE) and (B is LARGE) then (DECISION5)
Implement this expert system using neural networks. For each subunit
indicate clearly what are the connection weights and what
kind of output function(s) are used. Use only binary threshold
function at the neuron outputs. For threshold use connections
to +1
.
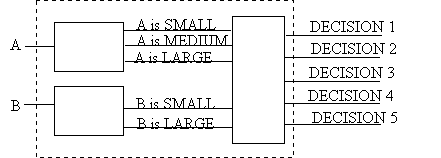
|
|
Q9)
Implement AND, OR and NOT Boole functions using bipolar
output Perceptron, for which the output function is
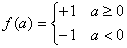
such
that +1 corresponds to True and –1 corresponds to False |
|
Q10)
Consider a two input bipolar perceptron
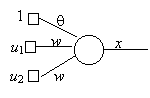 |
|
a)
For a two
input perceptron, a=0 defines a line on the two dimensional
input space (u1,u2), which divides
the input space into two halves such that the output is
+1 at one side while it is –1 on the other side. Draw
this line for q
= 0, w1=1, w2=2, and show on which
side of the line the output is
f(a)=1 and on which side f(a)=-1 |
|
b)
Examine how the line a=0 shifts
as q
changes and it rotates as w1 and w2
changes |
|
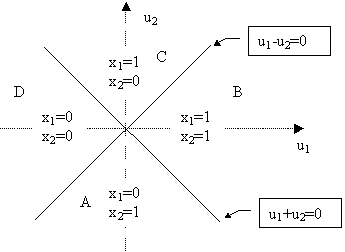
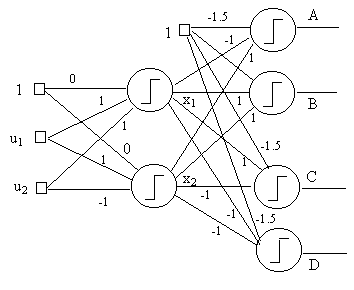
Q11)
Consider the network of bipolar perceptrons given above,
find out the lines defined by the first two neurons on
the input space (u1,u2). On each
region indicate the output value of each neuron.
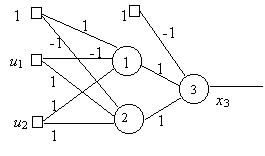
Design
a neural network
which will
perform the binary valued function given below
|
INPUT |
OUTPUT |
|
u1
u2 |
x |
|
1 1
-1 -1
-1 1
-1 -1 |
-1
1
1
-1 |
|
|
a) Indicate clearly the number
of neurons, the number of layers, the connections between
neurons, the connection weights, the output function |
|
b)
Draw the regions that the output of your network has value
-1 and 1 on two dimensional input space |
|
Q12)
Construct a continuous input, binary output multilayer
perceptron structure for classifying the elements
having the following distributions:
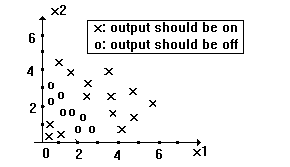 |
|
Q13)
Design a multilayer perceptron structure which produces
an output value1 if the applied input is from Class A
and produces 0 if it is from class B. Clearly indicate
connections and neuron characteristics.
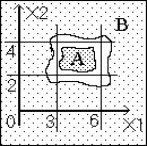
|
|
Q14)
Construct a continuous input, binary output multilayer
perceptron structure for classifying the elements
having the distributions: given below Clearly indicate
connections and neuron characteristics. |
|
a) Assign
an output neuron to each class.
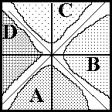
|
|
b) Use
a single output neuron such that x=1 for class A and x=0
for class B.
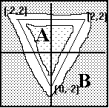
|
|
|
|
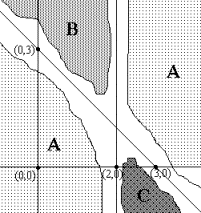
a)
|
|
Q15)
Construct a continuous input, binary output multilayer
perceptron structure having two output neurons to classify
the classes having
the following distributions:
|
|
Q16)
For a 2 dimensional input space,
let
Class
A=(inside of circle around (0,0) with radius 0.3);
Class
B= (inside of circle around (1,0) with radius 0.3);
Class
C=(inside of circle around (0,1) with radius 0.3);
|
|
a)
Show this classes on the input space |
|
b)
Draw 2 lines which seperates
these 3 classes |
|
c)
Design a multilayer perceptron structure which produces
output [1,0,0], [0,1,0] and [0,0,1] if the applied patern
is from the class A, B
and C respectively |
|
|
 |