|
EasyNumerics Software |
|
Solving Ordinary Differentiatial Equations (ODEs)
When you select the "Ordinary Differentiatial Equations" module from the main menu, the following window appears.
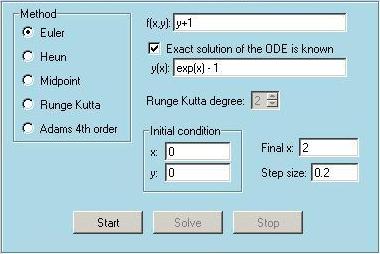
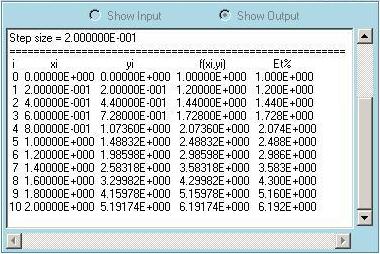
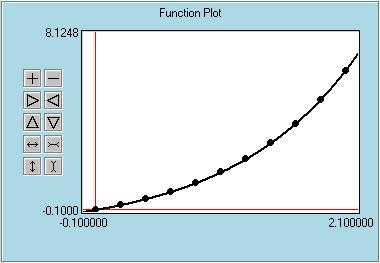
This module is used to solve initial value problems, which are first order Ordinary Differential Equations (ODEs) in the form of dy/dx=f(x,y). With this module it is possible to solve initial value problems using five different methods. The user can start the solution after selecting the method, initial condition and the step size. The results can be seen in the Output and the Function Plot windows. Note that except the 4th order Adams methods, all methods are self-starting. But 4th order Adams method is not self-starting, and the first three steps need to be computed with some other method. EasyNumerics uses the 4th order Runge-Kutta method for these steps. To help understanding the solution of ODEs, some snapshots taken during the solution dy/dx=y+1 in the interval [0,2] are shown below. The initial condition is given as y(0)=-1 and the step size is selected to be 0.2. These selections require the calculation of f and y at 10 different points. The second snapshot shows the results as written in the Output window. x, y, f(x,y) and percent true error values are shown at each calculation step. As shown, the errors grow as the solution progresses due to the accumulation of local errors. The third snapshot shows the results as plotted in the Function Plot window. The line corresponds to the specified exact solution. Points are the calculated y values. It is easy to experiment with different methods and step sizes and compare the solutions. For example the fourth snapshot shows the solution of the same problem with the 4th order Runge-Kutta method. The comparison of this result with the previous one clearly shows the improvement over the simple Euler method.
Please visit the movies section to watch sample runs of EasyNumerics. |