EasyNumerics Software

Home        Download & Installation        Screen Shots        Movies        Help        FAQ

How To Use The Software

Differentiation and Integration

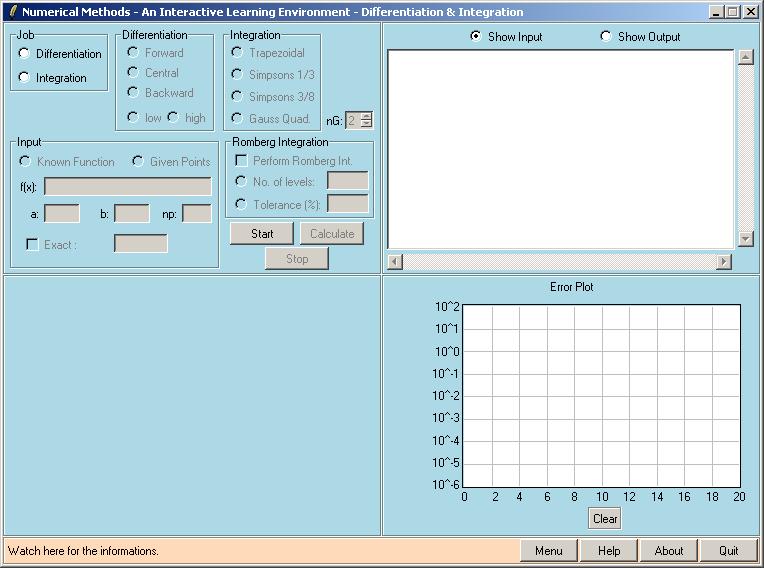
When you select the "Differentiation & Integration" module from the main menu, the following window appears.

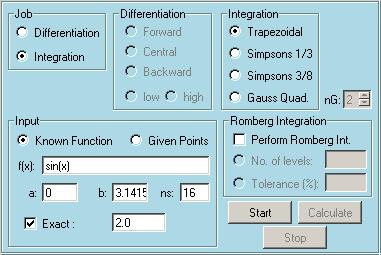
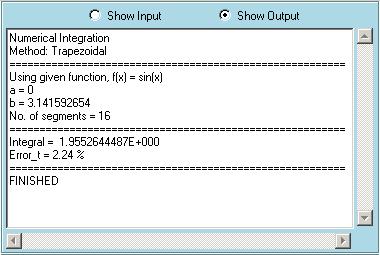
This module can be used to perform numerical differentiation and integration.

The user first selects the job, either differentiation or integration.

Forward, central and backward rules of two different orders can be used for differentiation. 1^st and 2^nd order formulas are used for forward and backward differentiation, whereas 2^nd and 4^th order formulas are used for central differentiation. Discrete data points can be entered by the user or they can be calculated from a known function.

For integration of discrete data points, there are three possibilities, Trapezoidal rule and two different Simpson’s rules. If the function is known, Gauss quadrature can be used for better accuracy. Another possibility for integrating known functions is the Romberg technique, the base of which is taken to be the Trapezoidal rule. The main advantage of the Romberg integration is its user defined stopping criteria. The user can select the levels of Romberg integration to be performed or specify a tolerance value as a stopping criteria of Romberg steps.

To help understanding the details of this module, some snapshots taken during a sample run that integrates sin(x) in the interval [0,p] using the Trapezoidal rule with 16 segments is shown below.

The first snapshot shows the entries, whereas the results are shown in the second one. Trapezoidal rule calculates this integral with a true percent relative error of 2.24 %. Although not shown here, the same integral can be calculated with a single segment three point Gauss quadrature formula with a true percent relative error of 0.07 %. The latter is more accurate and it uses less number of operations. For performance comparison purposes, it would be useful to know the number of floating point operations performed for each calculation, which can be implemented in the future releases of EasyNumerics.

Please visit the movies section to watch sample runs of EasyNumerics.