Bayesian Networks (BNs) are graphical models that represent the combined probability distribution among a group of variables (Pearl, 1988).
A BN consists of two parts, the graphical structure and the parameters. The graphical structure is a directional acyclic graph. Nodes in the graph represent variables, edges represent relationships between variables. If two nodes A and B in a BA are directly connected from A to B by an edge, then A is the parent of B and B is the child of A. Each node has parameters that define its conditional probability distribution with its parents. In discrete BNs, these parameters are defined in conditional probability tables.
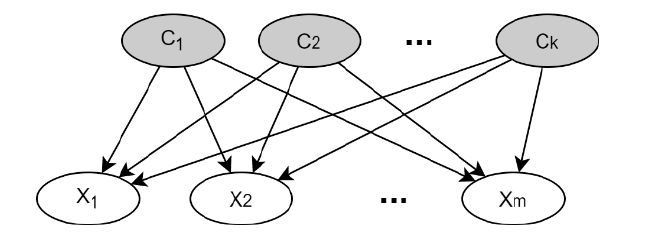
When a value is entered for any group of variables in the BN, the posterior probability distribution of other unknown variables can be calculated with inference algorithms such as a junction tree. The process of entering a value for a variable is also called entering evidence or entering an observation. With probabilistic inferences in the Bayes Network, predictive inference from parents to children, diagnostic inference from children to parents, or all-round inference between parents when the child is known can be calculated. When a value is entered into any set of questions in a PROM modeled as a BN, the posterior distributions of other questions and hidden factors can be calculated.
BNs can be made based on information, data, or a combination of the two. When the BN structure is made based on knowledge, the arrows in the model are determined according to the cause-effect relationships about the subject. BNs have structure learning algorithms to learn completely from data.
See the computerized adaptive testing page for more details on how to select most informative questions in PROM BNs.

