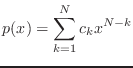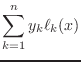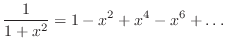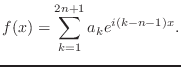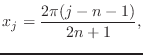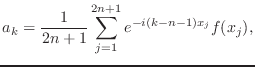MATH382: LAB 3: Interpolation on evenly-spaced Points



Introduction

This lab is concerned with interpolating data with polynomials and with trigonometric functions. There is a difference between interpolating and approximating. Interpolating means that the function passes through all the given points with no regard to the points between them. Approximating means that the function is close to all the given points and probably close to nearby points as well. It might seem that interpolating is always better than approximating, but there are many situations in which approximation is the better choice.

Polynomials are commonly used to interpolate data. There are several methods for defining, constructing, and evaluating the polynomial of a given degree that passes through data values. One common way is to solve for the coefficients of the polynomial by setting up a linear system called Vandermonde's equation. A second way is to represent the polynomial as the sum of simple Lagrange polynomials. Other ways are available and are discussed in the text and the lectures. In addition, we will discuss interpolation using trigonometric polynomials.

We will examine these two ways of finding the interpolating polynomial and a way of finding the interpolating trigonometric polynomial. We will see examples showing that interpolation does not necessarily mean good approximation and that one way that a polynomial interpolant can fail to approximate. Trigonometric polynomial interpolation does better, but can also break down.

Notation

This lab is focussed on finding functions that pass through certain specified points. In customary notation, you are given a set of points $ \{(x_k,y_k)\vert k=1,2,\ldots,n\}$and you want to find a function $ f(x)$that passes through each point ( $ f(x_k)=y_k$for $ k=1,2,\ldots,n$). That is, for each of the abscissę, $ x_k$, the function value $ f(x_k)$agrees with the ordinate $ y_k$. The given points are variously called the ``given'' points, the ``specified'' points, the ``data'' points, etc. In this lab, we will use the term ``data points.''

Written in the customary notation, it is easy to see that the quantities $ x$and $ x_k$are essentially different. In Matlab, without kerning and font differentiation, it can be difficult to keep the various quantities straight. In this lab, we will use the name xval to denote the values of $ x$and the names xdata and ydata to denote the data $ x_k$and $ y_k$. The variable names fval or yval are used for the value $ y=f(x)$to emphasize that it is an interpolated value.


Matlab Tips

At some point in this lab, you will need to determine if a quantity A is not equal to a quantity B. The Matlab syntax for this is

  if A ~= B

Sometimes it is convenient to enclose the logical expression in parentheses, but this is not required.

If you have a (square) linear system of equations, of the form

  A * x = b

where A is an N by N matrix, and b and x are column vectors, then Matlab can solve the linear system either by using the expression:

  x = inv(A)*b

or, better, via the ``backslash'' command:

  x = A \ b

that you used in the previous labs. The backslash command is strange looking. You might remember it by noting that the matrix A appears underneath the backslash. The backslash is used because matrix multiplication is not commutative, so a square matrix should appear to the left of a column vector. The difference between the two commands is merely that the backslash command is about three times faster because it solves the equation without constructing the inverse matrix. You will not notice a difference in this lab, but you might see one later if you use Matlab for more complicated projects.

The backslash command is actually more general than just multiplication by the inverse. It can find solutions when the matrix A is singular or when it is not a square matrix! We will discuss how it does these things later in the course, but for now, be very careful when you use the backslash operator because it can find ``solutions'' when you do not expect a solution.

Matlab has several commands for dealing with polynomials:

c=poly(r)

Finds the coefficients of the polynomial whose roots are given by the vector r.

r=roots(c)

Finds the roots of the polynomial whose coefficients are given by the vector c.

c=polyfit( xdata, ydata, n)

Finds the coefficients of the polynomial of degree n passing through, or approaching as closely as possible, the points xdata(k),ydata(k), for $ \texttt{k}=1,2,\dots,K$, where $ K-1$need not be the same as n.

yval=polyval( c, xval)

Evaluates a polynomial with coefficients given by the vector c at the values xval(k) for $ k=1,2,\dots,K$for $ K\ge 1$.

When there are more data values than the minimum, the polyfit function returns the coefficients of a polynomial that ``best fits'' the given values in the sense of least squares. This polynomial approximates, but does not necessarily interpolate, the data. In this lab, you will be writing m-files with functions similar to polyfit but that generate polynomials of the precise degree determined by the number of data points. (n=length(xdata)-1).

The vector of coefficients c of a polynomial in Matlab are, by convention, defined as

$\displaystyle p(x)=\sum_{k=1}^N c_k x^{N-k}$

(1)


Beware: When a vector of numbers, c, of length N, is regarded as coefficients of a polynomial of degree N-1, the subscripts run backwards! c(1) is the coefficient of the term with degree N-1, and the constant term is c(N).

In this and some later labs, you will be writing m-files with functions analogous to polyfit and polyval, using several different methods. Rather than following the matlab naming convention, functions with the prefix coef_ will generate a vector of coefficients, as by polyfit, and functions with the prefix eval_ will evaluate a polynomial (or other function) at values of xval, as with polyval.

In the this lab and often in later labs we will be using Matlab functions to construct a known polynomial and using it to generate ``data'' values. Then we use our interpolation functions to recover the original, known, polynomial. This strategy is a powerful tool for illustrative and debugging purposes, but practical use of interpolation starts from arbitrary data, not contrived data.


The Polynomial through Given Data


Vandermonde's Equation

Here's one way to see how to organize the computation of the polynomial that passes through a set of data.

Suppose we wanted to determine the linear polynomial $ p(x)=c_1x+c_2$that passes through the data points $ (x_1,y_1)$and $ (x_{2},y_{2})$. We simply have to solve a set of linear equations for $ c_1$and $ c_2$.

$\displaystyle c_1 x_1 + c_2$

$\displaystyle = y_1$

   

$\displaystyle c_1 x_2 + c_2$

$\displaystyle = y_2$

   


or, equivalently,

$\displaystyle \left[\begin{array}{cc}x_1 & 1 x_2 & 1\end{array}\right] \left[... ...c_1 c_2\end{array}\right]= \left[\begin{array}{c}y_1 y_2\end{array}\right] $

which (usually) has the solution

$\displaystyle c_1$

$\displaystyle =$

$\displaystyle ( y_2 - y_1 ) / ( x_2 - x_1 )$

 

$\displaystyle c_2$

$\displaystyle =$

$\displaystyle ( x_2 y_1 - x_1 y_2 ) / ( x_2 - x_1 )$

 


Compare that situation with the case where we want to determine the quadratic polynomial $ p(x) = c_1 x^2 + c_2 x + c_3$that passes through three sets of data values. Then we have to solve the following set of linear equations for the polynomial coefficients c:

$\displaystyle \left[\begin{array}{ccc}x_1^2 & x_1 & 1 [3pt] x_2^2 & x_2 & 1\... ...c_3\end{array}\right]= \left[\begin{array}{c}y_1 y_2 y_3\end{array}\right] $

This is an example of a third order Vandermonde Equation. It is characterized by the fact that for each row (sometimes column) of the coefficient matrix, the succesive entries are generated by a decreasing (sometimes increasing) set of powers of a set of variables.

You should be able to see that, for any collection of abscissę and ordinates, it is possible to define a linear system that should be satisfied by the (unknown) polynomial coefficients. If we can solve the system, and solve it accurately, then that is one way to determine the interpolating polynomial.

Now, let's see how to construct and solve the Vandermonde equation using Matlab. This involves setting up the coefficient matrix A. We use the Matlab variables xdata and ydata to represent the quantities $ x_k$and $ y_k$, and we will assume them to be row vectors of length n.

for j = 1:n

  for k = 1:n

    A(j,k) = xdata(j)^(n-k) ;

  end

end

Then we have to set the right hand side to the ordinates ydata, that is assumed to be a row vector. If we can get all of that set up, then actually solving the linear system is easy. We just write:

c = A \ ydata';

Recall that the backslash symbol means to solve the system with matrix A and right side ydata'. Notice that ydata' is the transpose of the row vector ydata in this equation. (By default, Matlab constructs row vectors unless told to do otherwise.)

Exercise 1: The Matlab built-in function polyfit finds the coefficients of a polynomial through a set of points. We will write our own using the Vandermonde matrix. (This is the way that the Matlab function polyfit works.)

1.      Write a Matlab function m-file, coef_vander.m with signature

2.  function c = coef_vander ( xdata, ydata )

3.  % c = coef_vander ( xdata, ydata )

4.  % xdata= ???

5.  % ydata= ???

6.  % c= ???

7.  % other comments

8.   

9.  % your name and the date

that accepts a pair of row vectors xdata and ydata of arbitrary but equal length, and returns the coefficient vector c of the polynomial that passes through that data. Be sure to complete the comments with question marks in them.
Warning: Think carefully about what to use for n.

10.  Test your function by computing the coefficients of the polynomial through the following data points. (This polynomial is $ y=x^2$, so you can check your coefficient vector ``by inspection.'')

11.xdata= [  0   1   2 ]

12.ydata= [  0   1   4 ]

13.  Test your function by computing the coefficients of the polynomial that passes through the following points

14.xdata= [  -3  -2 -1  0  1   2    3]

15.ydata= [1636 247 28  7  4  31  412]

16.  Confirm using polyval that your polynomial passes through these data points.

17.  Double-check your work by comparing with results from the Matlab polyfit function. Please include both the full polyfit command you used and the coefficient vector it returned in your summary.

In the following exercise you will construct a polynomial using coef_vander to interpolate data points and then you will see what happens between the interpolation points.

Exercise 2:

1.      Consider the polynomial whose roots are r=[-3 -2 -1 1 2]. Use the Matlab poly function to find its coefficients. Call these coefficients cTrue.

2.      This polynomial obviously passes through zero at each of these five ``data'' points. We want to see if our coef_vander function can reproduce it. To use our coef_vander function, we need a sixth point. You can ``read off'' the value of the polynomial at x=0 from its coefficients above. What is this value?

3.      Use the coef_vander function to find the coefficients of the polynomial passing through the ``data'' points

4.    xdata=[ -3 -2 -1 0  1 2 ];

5.    ydata=[  0  0  0 ?? 0 0 ];

Call these coefficients cVander.

6.      What coefficients would result from using only the five roots as xdata? Explain.

7.      Use the following code to compute and plot the values of the two polynomials on the interval [0,5]. If you look at the last line of the code, you will see an estimate of the difference between the two curves. How big is this difference? (We will be using essentially this same code in several following exercises. You should be sure you understand what it does. You might want to copy it to a script m-file.)

8.  xval=linspace(-3,2,4001);  % test abscissae for plotting

9.  yvalTrue=polyval(cTrue,xval);  % true ordinates

10.yvalVander=polyval(cVander,xval);  % our ordinates

11.plot(xval,yvalTrue,'b'); % true curve in blue

12.hold on

13.plot(xval,yvalVander,'r');  % our curve in red

14.hold off

15.max(abs((yvalTrue-yvalVander)))

Please include a copy of this plot with your summary. (If it appears that there is only one curve, it is possible that the red curve covers the blue one.)


Lagrange Polynomials

Suppose we fix the set of $ n$distinct abscissę $ x_k$, $ k=1,\ldots,n$and think about the problem of constructing a polynomial that has (not yet specified) values $ y_i$at these points. Now suppose I have a polynomial $ \ell_{7}(x)$whose value is zero at each $ x_k$, $ k\neq7$, and is 1 at $ x_{7}$. Then the intermediate polynomial $ y_{7} \ell_{7}(x)$would have the value $ y_{7}$at $ x_{7}$, and be 0 at all the other $ x_i$. Doing the same for each abscissa and adding the intermediate polynomials together results in the polynomial that interpolates the data without solving any equations!

In fact, the Lagrange polynomials $ \ell_k$are easily constructed for any set of abscissae. Each Lagrange polynomial will be of degree $ n-1$. There will be $ n$Lagrange polynomials, one per abscissa, and the $ k^{\mbox{th}}$polynomial $ \ell_{k}(x)$will have a special relationship with the abscissa $ x_{k}$, namely, it will be 1 there, and 0 at the other abscissę.

In terms of Lagrange polynomials, then, the interpolating polynomial has the form:

$\displaystyle p(x)$

$\displaystyle =$

$\displaystyle y_1 \ell_1(x) + y_2 \ell_2(x) +\ldots + y_n \ell_n(x)$

(2)

 

$\displaystyle =$

$\displaystyle \sum_{k=1}^n y_k\ell_k(x)$

 


Assuming we can determine these magical polynomials, this is a second way to define the interpolating polynomial to a set of data.

Remark: The strategy of finding a function that equals 1 at a distinguished point and zero at all other points in a set is very powerful. If $ y_k=1$in (2), then $ p(x)\equiv1$, so the $ \ell_k(x)$are an example of a ``partition of unity.'' One of the places you will meet it again is when you study the construction of finite elements for solving partial differential equations.

In the next two exercises, you will be constructing polynomials through the same points as in the previous exercise. Since there is only one nontrivial polynomial of degree (n-1) through n data points, the resulting interpolating polynomials are the same in these and the previous exercise.

In the next exercise, you will construct the Lagrange polynomials associated with the data points, and in the following exercise you will use these Lagrange polynomials to construct the interpolating polynomial.

Exercise 3: In this exercise you will construct Lagrange polynomials based on given data points. Recall the data set for $ y=x^2$:

   k :    1   2   3

xdata= [  0   1   2   ]

ydata= [  0   1   4   ]

(Actually, ydata is immaterial for construction of $ \ell_k(x)$.) In general, the formula for $ \ell_{k}(x)$can be written as:

$\displaystyle \ell_k(x)= (f_{1}(x)) (f_2(x)) \cdots (f_{k-1}(x)) (f_{k+1}(x)) \cdots (f_{n}(x) )$

(3)


(skipping the $ k^{\mbox{th}}$factor), where each factor has the form

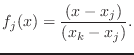
$\displaystyle f_{j}(x) = \frac{( x - x_{j} ) }{ ( x_{k} - x_{j})}. $

1.      Write a Matlab function m-file called lagrangep.m that computes the Lagrange polynomials (3) for any k. (One of the Matlab toolboxes has a function named ``lagrange'', so this one is named ``lagrangep''.) The signature should be

2.  function pval = lagrangep( k , xdata, xval )

3.  % pval = lagrangep( k , xdata, xval )

4.  % comments

5.  % k= ???

6.  % xdata= ???

7.  % xval= ???

8.  % pval= ???

9.   

10.% your name and the date

and the function should evaluate the k-th Lagrange polynomial for the abscissę xdata at the point xval. Hint, you can implement the general formula using code like the following.

pval = 1;

for j = 1 : ???

  if j ~= k

    pval = pval .* ???   % elementwise multiplication

  end

end

Note: If xval is a vector of values, then pval will be the vector of corresponding values, so that an elementwise multiplication (.*) is being performed.

11.  Look carefully at the definition of the Lagrange polynomials. From the definition alone, determine the values of lagrangep( 1, xdata, xval for xval=xdata(1), xval=xdata(2) and xval=xdata(3).

12.  Check Matlab results against yours. Does lagrangep give the correct values for lagrangep( 1, xdata, xdata)? For lagrangep( 2, xdata, xdata)? For lagrangep( 3, xdata, xdata)?

Exercise 4: The hard part is done. Now we want to use your lagrangep routine as a helper for a second replacement for polyfit-polyval pair, called eval_lag, that implements Equation (2). Unlike coef_vander, the coefficient vector of the polynomial does not need to be generated separately because it is so easy, and that is why eval_lag both fits and evaluates the Lagrange interpolating polynomial.

1.      Write a Matlab function m-file called eval_lag.m with the signature

2.  function yval = eval_lag ( xdata, ydata, xval )

3.  % yval = eval_lag ( xdata, ydata, xval )

4.  %  comments

5.   

6.  % your name and the date

This function should take the data values xdata and ydata, and compute the value of the interpolating polynomial at xval according to (2), using your lagrangep function for the Lagrange polynomials. Be sure to include comments to that effect.

7.      Test eval_lag on the simplest data set we have been using.

8.       k :    1   2   3

9.    xdata= [  0   1   2 ]

10.  ydata= [  0   1   4 ]

by evaluating it at xval=xdata. Of course, you should get ydata back.

11.  Test your function by interpolating the polynomial that passes through the following points, again by evaluating it at xval=xdata.

12.xdata= [  -3  -2 -1  0  1   2    3]

13.ydata= [1636 247 28  7  4  31  412]

14.  Repeat Exercise 2 using Lagrange interpolation.

o    Return to the polynomial constructed in Exercise 2 with roots r=[-3 -2 -1 1 2]. and coefficients cTrue.

o    Reconstruct (using polyval) or recall the ydata values associated with xdata=[-3 -2 -1 0 1 2].

o    Compute the values of the Lagrange interpolating polynomial at the same 4001 test points between -3 and 2. Call these values yvalLag.


Interpolating a function that is not a polynomial

Interpolating functions that are polynomials and using polynomials to do it is cheating a little bit. You have seen that interpolating polynomials can result in interpolants that are essentially identical to the original polynomial. Results can be much less satisfying when polynomials are used to interpolate functions that are not themselves polynomials. At the interpolation points, the function and its interpolant agree exactly, so we want to examine the behavior between the interpolation points. In the following exercise, you will see that some non-polynomial functions can be interpolated quite well, and in the subsequent exercise you will see one that cannot be interpolated well.  

Exercise 5: In this exercise you will construct interpolants for the function $ e^x$and see that it and its polynomial interpolant are quite close.

1.      We would like to interpolate the function $ y=e^x$on the interval $ [-\pi,\pi]$, so use the following outline to examine the behavior of the polynomial interpolant to the exponential function for five evenly-spaced points. It would be best if you put these commands into a script m-file named exer5.m.

2.  % construct n=5 data points

3.  n=5;

4.  xdata=linspace(-pi,pi,n);

5.  ydata=exp(xdata);

6.   

7.  % construct many test points

8.  xval=linspace(???,???,4001);

9.  % construct the true function, for reference

10.yvalTrue=exp(???);

11. 

12.% use Lagrange polynomial interpolation to evaluate

13.% the interpolant at the test points

14.yval=eval_lag(???,???,xval);

15. 

16.% plot reference values in blue, interpolant in red

17.plot(xval,yvalTrue,'b');

18.hold on

19.plot(xval,yval,'r');

20.hold off

21. 

22.% estimate the approximation error of the interpolant

23.approximationError=max(abs(yvalTrue-yval))

Please send me this plot.

24.  By zooming, etc., confirm visually that the exponential and its interpolant agree at the interpolation points.

25.  Using more data points gives higher degree interpolation polynomials. Fill in the following table using Lagrange interpolation with increasing numbers of data points.

26.  n =  5  Approximation Error = ________

27.  n = 11  Approximation Error = ________

28.  n = 21  Approximation Error = ________

You should have observed in Exercise 5 that the approximation error becomes quite small. The exponential function is entire, as are polynomials, so they share one essential feature. In the following exercise, you will see that interpolating functions that are not entire can give poor results.

Exercise 6:

1.      Construct a function m-file for the Runge example function $ y=\frac{1}{1+x^2}$. Name the file runge.m and give it the signature

2.  function y=runge(x)

3.  % y=runge(x)

4.  % comments

5.   

6.  % your name and the date

Use componentwise (vector) division and exponentiation (./ and .^).

7.      Copy exer5.m to exer6.m and modify it to use the Runge example function. Please send me the plot it generates.

8.      Confirm visually that the Runge example function and its interpolant agree at the interpolation points, but not necessarily between them.

9.      Using more data points gives higher degree interpolation polynomials. Fill in the following table using Lagrange interpolation with increasing numbers of data points.

10.  n =  5  Approximation Error = ________

11.  n = 11  Approximation Error = ________

12.  n = 21  Approximation Error = ________

13.  Are you surprised to see that the errors do not decrease?

Most people expect that an interpolating polynomial $ p(x)$gives a good approximation to the function $ f(x)$everywhere, no matter what function we choose. If the approximation is not good, we expect it to get better if we increase the number of data points. These expectations will be fulfilled only when the function does not exhibit some ``essentially non-polynomial'' behavior. You will see why the Runge example function cannot be approximated well by polynomials in the following exercise.

Exercise 7: The Runge example function has Taylor series

$\displaystyle \frac{1}{1+x^2}=1-x^2+x^4-x^6+\dots$

(4)


as you can easily prove. This series has a radius of convergence of 1 in the complex plane. Polynomials, on the other hand, are entire functions, i.e., their Taylor series' converge everywhere in the complex plane. No finite sum of polynomials can be anything but entire, but no entire function can interpolate the Runge example function on a disk with radius larger than one about the origin in the complex plane. If there were one, it would have to agree with the series (4) inside the unit disk, but the series diverges at $ x=i$and an entire function cannot have an infinite value.

1.      Make a copy of exer5.m called exer7.m that uses coef_vander and polyval to evaluate the interpolating polynomial rather than eval_lag.

2.      Confirm that you get the same results as in Exercise 6 when you use Vandermonde interpolation for the Runge example function.

3.    n =  5  Approximation Error = ________

4.    n = 11  Approximation Error = ________

5.    n = 21  Approximation Error = ________

6.      Look at the nontrivial coefficients ($ c_k$) of the interpolating polynomials by filling in the following table.

7.  n=5   c( 5)= _____  c( 3)= _____  c( 1)= _____

8.  n=11  c(11)= _____  c( 9)= _____  c( 7)= _____  c( 5)= _____

9.  n=21  c(21)= _____  c(19)= _____  c(17)= _____  c(15)= _____

10.limiting      +1            -1            +1            -1

11.  Look at the trivial coefficients ($ c_k$) of the interpolating polynomials by filling in the following table. (Look carefully at what the colon notation does.)

12.n=5   max(abs(c(2:2:end)))= _____

13.n=11  max(abs(c(2:2:end)))= _____

14.n=21  max(abs(c(2:2:end)))= _____

You should see that the interpolating polynomials are ``trying'' to reproduce the Taylor series (4). These polynomials cannot agree with the Taylor series at all points, though, because the Taylor series does not converge at all points.


Trigonometric polynomial interpolation

Quarteroni, Sacco, and Saleri discuss interpolation by trigonometric polynomials in Section 10.1. Trigonometric interpolation is closely related to approximation by Fourier series, but we will focus on interpolation in this lab.

The basic expression for trigonometric interpolation using $ (2n+1)$functions over the interval $ [-\pi,\pi]$is

$\displaystyle f(x)=\sum_{k=1}^{2n+1}a_ke^{i(k-n-1)x}.$

(5)


(We consider $ (2n+1)$points because we want to use real functions and real interpolants. Thus one trigonometric function $ e^{i(k-n-1)x}$is the constant term when $ k=n+1$, and all the rest come in complex conjugate pairs.)

Using the $ 2n+1$evenly-spaced points in the interval $ (-\pi,\pi)$given by

$\displaystyle x_j=\frac{2\pi(j-n-1)}{2n+1},$for $\displaystyle j=1,2,\dots,(2n+1),$

(6)


the coefficients can be determined from

$\displaystyle a_k=\frac{1}{2n+1}\sum_{j=1}^{2n+1}e^{-i(k-n-1)x_j}f(x_j),$    for $\displaystyle k=1,2,\dots,(2n+1).$

(7)


These equations can be found directly by multiplying (5) through by each of the functions $ e^{-i(k-n-1)x}$in turn, applying it to the values $ x_k$, and solving the resulting system for $ a_j$, taking advantage of the properties of the complex exponential to simplify the equations.



Remark: The trigonometric coefficients $ a_k$in (7) play the same role as the polynomial coefficients $ c_k$in (1).

In the following exercises, we are going to write functions coef_trig to be analogous to polyfit and coef_vander, and also eval_trig to be analogous to polyval and eval_lag.

Exercise 8:

1.      Construct a function m-file named coef_trig.m with the signature

2.  function a=coef_trig(f,n)

3.  % a=coef_trig(f,n)

4.  % f=???

5.  % n=???

6.  % a=???

7.  % comments

8.   

9.  % your name and the date

This function should evaluate the trigonometric coefficients $ a_k$according to Equation (7). Use Equation (6) to determine the points $ x_k$. It is more efficient to use vector (componentwise) notation and the Matlab sum function, but if you cannot see how to do that, just use for loops.

Hint: You can use the following code to generate the points $ x_k$without writing a for loop.

xdata = 2*pi*(-n:n)/(2*n+1);

Note: The length of a should be 2*n+1.

10.  Test your function by applying it to the function $ f(t)=e^{ix}$, for n=10. (You can either write an m-file for $ e^{ix}$or use Matlab's inline command. If you are using a recent version of Matlab, you can use the @ command to define an ``anonymous function.'') By examining Equation (5), you should be able to see that $ a_k=1$for $ k=n+2$and zero otherwise.

11.  Test your function again by applying it to $ f(x)=\sin 4x$with n=10. You should see that $ a_k$is zero for all but two subscripts. What subscripts ($ k$) have non-zero $ a_k$and what are the values?

Exercise 9:

1.      Construct a function m-file named eval_trig.m with the signature

2.  function fval=eval_trig(a,xval)

3.  % fval=eval_trig(a,xval)

4.  % a=???

5.  % xval=???

6.  % fval=???

7.  % comments

8.   

9.  % your name and the date

This function should evaluate Equation (5) at an arbitrary collection of points, xval.

10.  Test your function by first using coef_trig to find the coefficients for the function $ \sin 4x$with n=10 (you did this in the previous exercise), and then applying eval_trig to those coefficients at 4001 equally-spaced points in the interval $ [-\pi,\pi]$. Compare the interpolated values versus $ \sin 4x$. Plot them on the same plot: the lines should overlap. You can modify the m-file exer5.m that you wrote for Exercise 5. Call your modified m-file exer9.m. (Warning: Your interpolated values may appear to Matlab to be complex, and Matlab may not plot them the way you expect. In that case, verify that their imaginary parts (Matlab function imag) are zero and plot only the real (Matlab function real) parts. Please send me the plot.

Trigonometric polynomial interpolation does well even when the functions are not themselves trigonometric polynomials.

Exercise 10:

1.      Modify exer9.m to use the function $ y=x(\pi^2-x^2)$, and call the modified file exer10.m. Plot the function and its interpolant for n=5, 10, 15 and n=20. You do not have to send me the plots, but fill in the following table.

2.    n =  5 x.*(pi^2-x.^2) Approximation Error = ________

3.    n = 10 x.*(pi^2-x.^2) Approximation Error = ________

4.    n = 15 x.*(pi^2-x.^2) Approximation Error = ________

5.    n = 20 x.*(pi^2-x.^2) Approximation Error = ________

6.      Do the same thing for the Runge example function and fill in the following table.

7.    n = 2  Runge Approximation Error = ________

8.    n = 4  Runge Approximation Error = ________

9.    n = 5  Runge Approximation Error = ________

You do not have to send me the plots.

10.  For the n=2 case, and the Runge example function, the five points at which the trigonometric interpolation should interpolate the Runge example function are

11.xval=2*pi*(-2:2)/5;

Check that runge and eval_trig agree at those points.

The previous exercise shows that trigonometric polynomial interpolation does well for some functions. It does much less well when the function is not continuous or not periodic in $ [-\pi,\pi]$. Consider, for example, the function

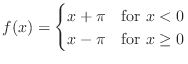
$\displaystyle f(x)=\begin{cases}x+\pi & \text{for } x<0\\ x-\pi & \text{for } x\ge0 \end{cases} $

Exercise 11:

1.      Copy the following code into a function m-file named sawshape6.m

2.  function y=sawshape6(x)

3.  % y=sawshape6(x)

4.  % x=???

5.  % y=???

6.  % comments

7.   

8.  % your name and the date

9.   

10.kless=find(x<0);

11.kgreater=find(x>=0);

12.y(kless)=x(kless)+pi;

13.y(kgreater)=x(kgreater)-pi;

Be sure to add the usual comments.

14.  The Matlab find command is a very useful function. Use the help find command or the Help facility to see what it does.

15.  If x=[0 1 2 3 4 5 6 7 8 9 8 7 6], what is the result of the function calls find(x==2), find(x==7), and find(x>5)?

16.  Use a script file based on exer9.m to fill in the following table by interpolating the sawshape6 function using trigonometric interpolation.

17.  n =   5  Approximation Error = ________

18.  n =  10  Approximation Error = ________

19.  n = 100  Approximation Error = ________

You can see that the approximation error is not shrinking, but if you look at the plots you will see that the error really is shrinking everywhere except near zero, where the oscillations get more rapid but do not get smaller. This behavior is typical and is called Gibbs's phenomenon. Please send me only the plot for n=100.

Increasing the order of polynomial interpolation can lead to divergence of approximation because of ``the wiggles.'' Trigonometric interpolation does not diverge as $ n\rightarrow\infty$, but Gibbs phenomenon keeps the approximation from converging at discontinuities.