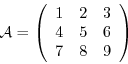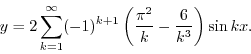MATH2070: LAB 2: Beginning Matlab

MATH382: LAB 2: Beginning Matlab

Introduction

In the last lab, we learned how to start up Matlab and a little bit about using Matlab. Matlab is a programming language and it is important to learn the basics of good programming so that you will be able to use Matlab for research and applications.

Matlab files

The best way to use Matlab is to use its scripting (programming) facility. With sequences of Matlab commands contained in files, it is easy to see what calculations were done to produce a certain result, and it is easy to show that the correct values were used in producing a graph. When the commands are in clear text files, with easily read, well-commented code, you have a very good idea of how a particular result was obtained. And you will be able to reproduce it and similar calculations as often as you please.

The Matlab comment character is a percent sign (%). That is, lines starting with % are not read as Matlab commands and can contain any text. Similarly, any text on a line following a % can contain textual comments and not Matlab commands. It is important to include comments in script and function files to explain what is being accomplished.

Matlab commands are sometimes terminated with a semicolon (;) and sometimes not. The difference is that the result of a calculation is printed to the screen when there is no semicolon but no printing is done when there is a semicolon. It is a good idea to put semicolons at the ends of all calculational lines in a function file.

There are three kinds of files that Matlab can use:

1. Script files (or ``m-files''),

2. Function files (or ``m-files'') and

3. Data files.

Script m-files

A Matlab script m-file is a text file with the extension .m. Matlab script files should always start off with comments that identify the author, the date, and a brief description of the intent of the calculation that the file performs. Matlab script files are invoked by typing their names without the .m at the Matlab command line or by using their names inside another Matlab file. Invoking the script causes the commands in the script to be executed, in order.

Function m-files

Matlab function files are also text files with the extension .m, but the first non-comment line must start with the word function and be of the form

function output variable = function name (parameters)

For example, the function that computes the sine would start out

function y=sin(x)

and the name of the file would be sin.m. The defining line, starting with the word function is called the ``signature'' of the function. If a function has no input parameters, they, and the parentheses, can be omitted. Similarly, a function need not have output parameters. The name of the function must be the same as the file name. It is best to have the first line of the function m-file be the signature line, starting with the word ``function.'' The lines following the signature should always contain comments with the following information.

1. Repetition of the signature of the function (useful as part of the help message),

2. A brief description of the intent of the calculation the function performs,

3. Brief descriptions of the input and output variables, and,

4. The author's name and date.

Part of the first of these lines is displayed in the ``Current directory'' windowpane, and the lines themselves comprise the response to the Matlab command help function name.

The key differences between function and script files are that

Functions are intended to be used repetitively,
Functions can accept parameters, and,
Variables used inside a function are invisible outside the function.

This latter point is important: variables used inside a function (except for output variables) are invisible after the function completes its tasks while variables in script files remain in the workspace.

When I am working on a task, I often start out using script files. As I discover just what tasks are repetitive or when I start to need the same calculation repeated for different parameters, or when I have many intermediate variables that might have the same names as variables in other parts of the calculation, I switch to function files. In these labs, I will specify function file or script file when it is important, and you are free to use what you like when I do not specify.

Because function files are intended to be used multiple times, it is a bad idea to have them print or plot things. Imagine what happens if you have a function that prints just one line of information that you think might be useful, and you put it into a loop that is executed a thousand times. Do you plan to read those lines?

Note: Matlab function names are case-sensitive. This means that the function cos is different from Cos, coS, and COS. File names in Microsoft operating systems, however, are not strictly case sensitive. To avoid confusion for those students who might be using Matlab on a Microsoft system, in these labs we will only use lower-case names for Matlab function and script files.

Data files

Matlab also supports data files. The Matlab save command will cause every variable in the workspace to be saved in a file called ``matlab.mat''. You can also name the file with the command save filename that will put everything into a file named ``filename.mat''. This command has many other options, and you can find more about it using the help facility. The inverse of the save command is load.

Variables

Matlab uses variable names to represent data. A variable name represents a matrix containing complex double-precision data. Of course, if you simply tell Matlab x=1, Matlab will understand that you mean a $1\times1$ matrix and it is smart enough to print x out without its decimal and imaginary parts, but make no mistake: they are there. And xcan just as easily turn into a matrix.

A variable can represent some important value in a program, or it can represent some sort of dummy or temporary value. Important quantities should be given names longer than a few letters, and the names should indicate the meaning of the quantity. For example, if you were using Matlab to generate a matrix containing a table of squares of numbers, you might name the table tableOfSquares. (The convention I am using here is that the first part of the variable name should be a noun and it should be lower case. Modifying words follow with upper case letters separating the words. This rule comes from the officially recommended naming of Java variables.)

Once you have used a variable name, it is bad practice to re-use it to mean something else. It is sometimes necessary to do so, however, and the statement

clear variableOne variableTwo

should be used to clear the two variables variableOne and variableTwo before they are re-used. This same command is critical if you re-use a variable name but intend it to have smaller dimensions.

Matlab has a few reserved variable names. You should not use these variables in your m-files. If you do use such variables as i or pi, they will lose their special meaning until you clear them. Reserved names include

ans: The result of the previous calculation.

computer: The type of computer you are on.

eps: The smallest positive number $\epsilon$ that both satisfies the expression $1+\epsilon>1$ and can be represented on this computer.

i, j: The imaginary unit ( $\sqrt{-1}$ ). In this course you should avoid using i or j as subscripts or loop indices.

inf: Infinity ( $\infty$ ). This will be the result of dividing 1 by 0.

NaN: ``Not a Number.'' This will be the result of dividing 0 by 0, or inf by inf, multiplying 0 by inf, etc.

pi: $\pi$

realmax, realmin: The largest and smallest real numbers that can be represented on this computer.

version: The version of Matlab you are running.

Exercise 1: Start up Matlab and use it to answer the following questions. Do not forget to open the diary file by using the command ``diary diary.txt''.

1. What are the values of the reserved variables pi, eps, realmax, and realmin?

2. Use the ``format long'' command to display pi in full precision and ``format short'' to return Matlab to its default, short, display.

3. No matter how it is printed, the internal precision of any variable is always about 15 decimal digits. The value for pi printed in short format is 3.1416. What ispi-3.1416? You should see that this value is not zero. You found the value of pi printed using format long in the previous part of this exercise. What is the difference between the printed value and pi? This value is also not zero, but it is much smaller than the value of pi-3.1416.

4. Set the variable a=1, the variable b=1+eps, and the variable c=2+eps. What is the difference in the way that Matlab displays these values? Can you tell from the form of the printed value that a and b are different?

5. Will the command format long cause all the decimal places in b to be printed, or is there still some missing precision?

6. Choose a value and set the variable x to that value.

7. What is the square of x? Its cube?

8. Choose an angle $\theta$ and set the variable theta to its value (a number).

9. What is $\sin\theta$ ? $\cos\theta$ ? Angles can be measured in degrees or radians. Which of these has Matlab used?

10. Matlab variables can also be given ``character'' or ``string'' values. A string is a sequence of letters, numbers, spaces, etc., surrounded by single quotes ('). In your own words, what is the difference between the following two expressions?

11. a1='sqrt(4)'

12. a2=sqrt(4)

13. The Matlab eval function is used to EVALuate a string as if it were typed at the command line. If a1 is the string given above, what is the result of the commandeval(a1)? Of a3=5*eval(a1)?

14. Use the save command to save all your variables. Check your ``Current Directory'' to see that you have created the file matlab.mat.

15. Use the clear command. Check that there are no variables left in the ``current workspace'' (windowpane is empty).

16. Restore all the variables with load and check that the variables have been restored to the ``Current workspace'' windowpane.

Vectors and matrices

We said that Matlab treats all its variables as though they were matrices. Important subclasses of matrices include row vectors (matrices with a single row and possibly several columns) and column vectors (matrices with a single column and possibly several rows). One important thing to remember is that you don't have to declare the size of your variable; Matlab decides how big the variable is when you try to put a value in it. The easiest way to define a row vector is to list its values inside of square brackets, and separated by spaces or commas:

rowVector = [ 0, 1, 3, -6, pi ]

The easiest way to define a column vector is to list its values inside of square brackets, separated by semicolons or line breaks.

columnVector1 = [ 0; 1; 3; -6; pi ]

columnVector2 = [ 0

100 ]

(It is not necessary to line the entries up as I have done, but it makes it look nicer.) Note that rowVector is not equal to columnVector1 even though each of their components is the same.

Matrices can be written using both commas and semicolons. The matrix

$\begin{displaymath} \mathcal{A}=\left( \begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{array}\right) \end{displaymath}$

(1)

can be generated with the expression

A=[1,2,3;4,5,6;7,8,9]

or, more clearly, as

A=[ 1 2 3

4 5 6

7 8 9];

Matlab has a special notation for generating a set of equally spaced values, which can be useful for plotting and other tasks. The format is:

start : increment : finish

start : finish

in which case the increment is understood to be 1. Both of these expressions result in row vectors. So we could define the even values from 10 to 20 by:

evens = 10 : 2 : 20

Sometimes, you'd prefer to specify the number of items in the list, rather than their spacing. In that case, you can use the linspace function, which has the form

linspace( firstValue, lastValue, numberOfValues )

in which case we could generate six even numbers with the command:

evens = linspace ( 10, 20, 6 )

or fifty evenly-spaced points in the interval [10,20] with

points = linspace ( 10, 20, 50 )

As a general rule, use the colon notation when the increment is an integer or when you know what the increment is and use linspace when you know the number of values but not the increment.

Another nice thing about Matlab vector variables is that they are flexible. If you decide you want to add another entry to a vector, it's very easy to do so. To add the value 22 to the end of our evens vector:

evens = [ evens, 22 ]

and you could just as easily have inserted a value 8 before the other entries, as well.

Even though the number of elements in a vector can change, Matlab always knows how many there are. You can request this value at any time by using the length function. For instance,

length ( evens )

should yield the value 7 (the 6 original values of 10, 12, ... 20, plus the value 22 tacked on later). In the case of matrices with more than one nontrivial dimension, the lengthfunction returns the total number of entries. the size function returns a vector containing two values: the number of rows and the number of columns. To get the number of rows of a variable v, use size(v,1) and to get the number of columns use size(v,2). For example, since evens is a row vector, size( evens, 1)=1 and size( evens, 2)=7, one row and seven columns.

To specify an individual entry of a vector, you need to use index notation, which uses round parentheses enclosing the index of an entry. The first element of an array has index 1 (as in Fortran, but not C or Java). Thus, if I want to alter the third element of evens, I could say

evens(3) = 7

Exercise 2:

1. Use the linspace function to create a row vector called meshPoints containing exactly 1000 values with values evenly spaced between -1 and 1. Do not print all 1000 values!

2. What expression will yield the value of the $55^{\mbox{th}}$ element of meshPoints? What is this value?

3. Double-click on the variable meshPoints in the ``Current workspace'' windowpane to view it as a vector and confirm its length is 1000.

4. Use the length function to again confirm the vector has length 1000.

5. Produce a plot of a sinusoid on the interval using the command

6. plot(meshPoints,sin(2*pi*meshPoints))

Please save (export) this plot as a jpeg (.jpg) file and send it along with your summary. The command line expression to save a plot is

print -djpeg plotname.jpg

where ``plotname.jpg'' is a name you choose for the file.
Remarks:

o Although these files are typically written with an .jpg extension, the print command uses the 4-letter description ``jpeg''.

o There are many other graphical file formats that Matlab can produce. Please use only ``jpeg'' format in these labs.

7. Create a file named exer2.m. You can use the Matlab command edit, type the above commands into the window and use ``Save as'' to give it a name, or you can highlight some commands in the history windowpane and use a right mouse click to bring up a menu to save the commands as an m-file. The first lines of the file should be the following:

8. % Lab 2, exercise 2

9. % A sample script file.

10. % Your name and the date

Follow the header comments with the commands containing exactly the commands you used in the earlier parts of this exercise. Test your script by using clearto clear your results and then execute the script from the command line by typing exer2.

Vector and matrix operations

Matlab provides a large assembly of tools for matrix and vector manipulation. We will investigate a few of these by trying them out.

Exercise 3: Define the following vectors and matrices:

rowVec1 = [ -1 -4 -9]

colVec1 = [ 2

8 ]

mat1 = [ 1 3 5

7 9 0

2 4 6 ]

1. You can multiply vectors by constants. Compute

2. colVec2 = (pi/4) * colVec1

3. The cosine function can be applied to a vector to yield a vector of cosines. Compute

4. colVec2 = cos( colVec2 )

Note that the values of colVec2 have been overwritten. Are these the values you expect?

5. You can add vectors. Compute

6. colVec3 = colVec1 + colVec2

7. Matlab will not allow you to do illegal operations! Try to compute

8. illegal = colVec1 + rowVec1;

Look carefully at the error message. You must recognize from the message what went wrong when you see it in the future.

9. The Euclidean norm of a matrix or a vector is available using norm. Compute

10. norm(colVec3)

11. You can do row-column matrix multiplication. Compute

12. colvec4 = mat1 * colVec1

13. A single quote following a matrix or vector indicates a transpose.

14. mat1Transpose = mat1'

15. rowVec2 = colVec3'

Warning: The single quote really means the complex-conjugate transpose (or Hermitian adjoint). If you want a true transpose applied to a complex matrix you must use ``.'''.

16. Transposes allow the usual operations. You might find ${\bf u}^T{\bf v}$ a useful expression to compute the dot (inner) product ${\bf u}\cdot{\bf v}$ (although there is a dot function in Matlab).

17. mat2 = mat1 * mat1' % symmetric matrix

18. rowVec3 = rowVec1 * mat1

19. dotProduct = colVec3' * colVec1

20. euclideanNorm = sqrt(colVec2' * colVec2)

21. Matrix operations such as determinant and trace are available, too.

22. determinant = det( mat1 )

23. tr = trace( mat1 )

24. You can pick certain elements out of a vector, too. Use the following command to find the smallest element in a vector rowVec1.

25. min(rowVec1)

26. The min and max functions work along one dimension at a time. They produce vectors when applied to matrices.

27. max(mat1)

28. You can compose vector and matrix functions. For example, use the following expression to compute the max norm of a vector.

29. max(abs(rowVec1))

30. How would you find the single largest element of a matrix?

31. As you know, a magic square is a matrix all of whose row sums, column sums and the sums of the two diagonals are the same. (One diagonal of a matrix goes from the top left to the bottom right, the other diagonal goes from top right to bottom left.) Consider the matrix

32. A=magic(100); % please do not print all 10,000 entries.

The matrix A has 100 row sums (one for each row), 100 column sums (one for each column) and two diagonal sums. These 202 sums should all be exactly the same, and you could verify that they are the same by printing them and ``seeing'' that they are the same. It is easy to miss small differences among so many numbers, though. Instead, verify that A is a magic square by constructing the 100 column sums (without printing them) and computing the maximum and minimum values of the column sums. Do the same for the 100 row sums, and compute the two diagonal sums. Check that these six values are the same. If the maximum and minimum values are the same, the flyswatter principle says that all values are the same.

Hints:

o Use the Matlab min and max functions.

o Recall that sum applied to a matrix yields a row vector whose values are the sums of the columns.

o The Matlab function diag extracts the diagonal of a matrix, and the composed function sum(diag(fliplr(A))) computes the sum of the other diagonal.

33. Suppose we want a table of integers from 0 to 13, their squares and cubes. We could start with

34. integers = 0 : 13

but now we'll get an error when we try to multiply the entries of integers by themselves.

squareIntegers = integers * integers

Realize that Matlab deals with vectors, and the default multiplication operation with vectors is row-by-column multiplication. What we want here is element-by-element multiplication, so we need to place a period in front of the operator:

squareIntegers = integers .* integers

Now we can define cubeIntegers and fourthIntegers in a similar way.

cubeIntegers = squareIntegers .* integers

fourthIntegers = squareIntegers .* squareIntegers

Finally, we would like to print them out as a table. integers, squareIntegers, etc. are row vectors, so make a matrix whose columns consist of these vectors and allow Matlab to print out the whole matrix at once.

tableOfPowers=[integers', squareIntegers', cubeIntegers', fourthIntegers']

35. Watch out when you use vectors. The multiplication, division and exponentiation operators all have two possible forms, depending on whether you want to operate on the arrays, or on the elements in the arrays. In all these cases, you need to use the period notation to force elementwise operations. Compute the squares of the values in integers alternatively using the exponentiation operator as:

36. sqIntegers = integers .^ 2

and check that the two calculations agree with the command

norm(sqIntegers-squareIntegers)

which should result in zero.

Remark: Addition, subtraction, and division or multiplication by a scalar never require the dot in front of the operator, although you will get the correct result if you use one.

37. The index notation can also be used to refer to a subset of elements of the array. With the start:increment:finish notation, we can refer to a range of indices. Two-dimensional vectors and matrices can be constructed by leaving out some elements of our three-dimensional ones. For example, submatrices an be constructed from tableOfPowers. (The end function in Matlab means the last value of that dimension.)

38. tableOfCubes = tableOfPowers(:,[1,3])

39. tableOfEvenCubes = tableOfPowers(1:2:end,[1,3])

40. tableOfOddFourths = tableOfPowers(2:2:end,1:3:4)

Note: [1:3:4] is the same as [1,4].

41. You have already seen the Matlab function magic(n). Use it to construct a $10\times10$ matrix.

42. A = magic(10)

Flow control

It is critical to be able to ask questions and to perform repetitive calculations in m-files. These topics are examples of ``flow control'' constructs in programming languages. Matlab provides two basic looping (repetition) constructs: for and while, and the if construct for asking questions. These statements each surround several Matlab statements with for, while or if at the top and end at the bottom.

Note: It is an excellent idea to indent the statements between the for, while, or if lines and the end line. This indentation strategy makes code immensely more readable. Your m-files will be expected to follow this convention.

Syntax

Example

for loop

for control-variable=start : increment : end

Matlab statement ...

...

end

nFactorial=1;

for i=1:n

nFactorial=nFactorial*i;

end

while loop

Matlab statement initializing a control variable

while logical condition involving the control variable

Matlab statement ...

...

Matlab statement changing the control variable

end

nFactorial=1;

i=1; % initialize i

while i <= n

nFactorial=nFactorial*i;

i=i+1;

end

a simple if

if logical condition

Matlab statement ...

...

end

if x ~= 0 % ~ means "not"

y = 1/x;

end

a compound if

if logical condition

Matlab statement ...

...

elseif logical condition

...

else

...

end

if x ~= 0

y=1/x;

elseif x > 0

y = +inf;

else

y = -inf;

end

Note that elseif is one word! Using two words else if changes the statement into two nested if statements with possibly a very different meaning, and a different number of end statements.

Exercise 4: The trapezoid rule for the approximate value of the integral of on the interval can be written as

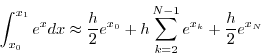
$\begin{displaymath} \int_{x_0}^{x_1}e^xdx\approx \frac{h}2e^{x_0} + h\sum_{k=2}^{N-1}e^{x_k}+\frac{h}2e^{x_N} \end{displaymath}$

where and $x_k=0,k,2k,\ldots,1$ .

The following Matlab code computes the trapezoid rule for the case that , and .

% Use the trapezoid rule to approximate the integral from 0 to 1

% of exp(x), using N (=25) intervals

% Your name and the date

N=25;

h=1/(N-1);

x=-h; % look at this trick

approxIntegral=0.;

for k=1:N

% compute current x value

x=x+h;

% add the terms up

if k==1 | k==N

approxIntegral=approxIntegral+(h/2)*exp(x); % ends of interval

else

approxIntegral=approxIntegral+h*exp(x); % middle of interval

end

1. Use cut-and-paste to put the code directly into the Matlab command window to execute it. Is the final value for approxIntegral nearly equal to ? (You can get the value of a variable by simply typing its name at the command prompt.)

2. Notice the indentation. Typically, statements inside for loops and if tests are indented for readability. (There isn't much to be gained by indentation when you are typing at the command line, but when you put commands in a file you should always use indentation.)

3. What is the complete sequence of all values taken on by the variable x?

4. How many times is the following statement executed?

5. approxIntegral=approxIntegral+(h/2)*exp(x); % ends of interval

6. How many times is the following statement executed?

7. approxIntegral=approxIntegral+h*exp(x); % middle of interval

M-files and graphics

If you have to type everything at the command line, you will not get very far. You need some sort of scripting capability to save the trouble of typing, to make editing easier, and to provide a record of what you have done. You also need the capability of making functions or your scripts will become too long to understand. In this section we will consider first a script file and later a function m-file. We will be using graphics in the script file, so you can pick up how graphics can be used in our work.

The Fourier series for the function on the interval $-1\le x\le 1$ is

$\begin{displaymath} y=2\sum_{k=1}^\infty (-1)^{k+1}\left (\frac{\pi^2}{k}-\frac{6}{k^3}\right)\sin kx. \end{displaymath}$

(2)

We are going to look at how this series converges.

Exercise 5: Copy and paste the following text into a file named exer5.m and then answer the questions about the code.

% compute NTERMS terms of the Fourier Series for y=x^3

% plot the result using NPOINTS points from -1 to 1.

% Your name and the date

NTERMS=10;

NPOINTS=1000;

x=linspace(-1,1,NPOINTS);

y=zeros(size(x));

for k=1:NTERMS

y=y-2*(-1)^k*(pi^2/k-6/k^3)*sin(k*x);

end

plot(x,y);

hold on

plot(x,x.^3,'g');

axis([-1,1,-2,2]);

hold off

It is always good programming practice to define constants symbolically at the beginning of a program and then to use the symbols within the program. Sometimes these special constants are called ``magic numbers.'' By convention, symbolic constants are named using all upper case.

1. Add your name and the date to the comments at the beginning of the file.

2. How is the Matlab variable x related to the dummy variable in Equation (2)? (Please use no more than one sentence for the answer.)

3. How is the Matlab statement that begins y=y... inside the loop related to the summation in Equation (2)? (Please use no more than one sentence for the answer.)

4. In your own words, what does the line

5. y=zeros(size(x));

do? Hint: You can use Matlab help for zeros and size for more information.

6. Execute the script by typing its name exer5 at the command line. You should see a plot of two lines, one representing a partial sum of the series and the green line a plot of , the limit of the partial sums. You do not have to send me this plot.

7. What would happen if the two lines hold on and hold off were omitted?

Note: The command hold, without the ``on'' or ``off'', is a ``toggle.'' Each time it is used, it switches from ``on'' to ``off'' or from ``off'' to ``on.'' Using it that way is easier but you have to remember which state you are in.

In the following exercise you are going to modify the calculation so that it continues to add terms so long as the difference between the partial sum and the function is larger than, say, 0.1. The while statement is designed for this case. It would be used in the following way, replacing the for statement.

TOLERANCE=0.1; % the chosen tolerance value

<<some lines of code from above>>

k=0;

difference=TOLERANCE+1; % bigger than TOLERANCE

while difference > TOLERANCE

k = k + 1;

<<some lines of code from above>>

difference = max( abs( x.^3 - y ) );

end

disp( strcat('Number of iterations =',num2str(k)) )

<<some lines of code to plot results>>

Exercise 6:

1. Copy the file exer5.m to a new file called exer6.m or use ``Save as'' from the File menu. Change the comments at the beginning of the file to reflect the objective of this exercise.

2. Modify exer6.m by a replacing the for loop with a while loop as outlined above.

3. What is the purpose of the statement

4. difference=TOLERANCE+1;

5. What is the purpose of the statement

6. k = k + 1;

7. Try the script to see how it works. How many iterations are required?

Hint: If you try this script and it does not quit (it stays ``busy'') you can interrupt the calculation by holding the Control key (``CTRL'') and pressing ``C''. If this doesn't seem to work, open the blank window that opened and was minimized when you started Matlab and use CTRL-C key combination in that window.

If you find that your code does not quit, you have a bug. For some reason, the value of the variable difference is not getting small. Look at your code carefully to find out why. If you cannot see it, use the debugger to watch execution and see what is happening to the value of difference.

The next task is to make a function m-file out of exer6.m in such a way that it takes as argument the desired tolerance and returns the number of iterations required to meet that tolerance.

Exercise 7:

1. Copy the file exer6.m to a new file called exer7.m, or use ``Save As'' from the File menu. Turn it into a function m-file by placing the signature line first and adding a comment for its usage

2. function k = exer7( tolerance )

3. % k = exer7( tolerance )

4. % more comments

5. % Your name and the date

6. Replace the upper-case TOLERANCE with a lower-case tolerance because it no longer is a constant, and throw away the line giving it a value.

7. Note that the function name must agree with the file name. Add comments just after the signature and usage lines to indicate what the function does.

8. Delete the lines that create the plot and print (disp(...)) so that the function does its work silently.

9. Invoke this function from the Matlab command line by choosing a tolerance and calling the function. Using the command

10. exer7(0.1)

will cause Matlab to print the result. Using the function on the right side of an equal sign with a variable on the left side of the equal sign causes the variable to take the value given by the function.

numItsRequired=exer7(0.1)

causes both a printed value and assignment of a value to numItsRequired.

11. Use the command help exer7 to display your help comments. Make sure they describe the purpose of the function.

12. How many iterations are required for a tolerance of 0.1? For a tolerance of 0.05? For a tolerance of 0.025? For a tolerance of 0.0125?

Unlike ordinary mathematical notation, Matlab allows a function to return two or more values instead of a single value. The syntax to accomplish this trick is similar to that of defining a vector, but the meaning is nothing like a vector. For a function named ``func'' that returns two variables depending on a single variable as input, the signature line would look like:

[y,z] = func( x )

and to use the function, for the value at x = 3,

[y,z] = func( 3 )

If you have the same function but wish only the first output variable, y, you would write

y = func( 3 )

and if you wish only the second output variable, z, you would write

[~,z] = func( 3 )

Warning: The ~ notation works only on recent versions of Matlab and not on the version in GSCC.

Exercise 8:

1. Copy the file exer7.m to a new file called exer8.m, or use ``Save As'' from the File menu. Modify the function so that it returns first the converged value of the sum and, second, the number of iterations required. Be sure to change the comments to include a description of all input and output parameters.

2. What form of the command line would return only the the value of the sum to a tolerance of 0.03. What is this value, using format long to get at least 14 digits of accuracy?

3. What form of the command line would return both the value of the sum and the number of iterations required to achieve a tolerance of 0.02? How many iterations were taken, and what is the value of the sum, using format long to get at least 14 digits of accuracy?

You have now completed all the required work for this lab. There is an extra credit exercise below. If you wish to gain the extra credit, do that exercise now.

When you have finished your work, be sure to send it to me. It should include your summary file, the diary.txt file, each of the m-files exer2.m, exer5.m, exer6.m,exer7.m, exer8.m and the plot files (.jpg) files you created. Also include your extra credit work if you chose to do it. Remember that you can zip all these files in your area from the Matlab command line with the command

!zip filename.zip *.m *.txt *.jpg

where filename.zip is a file name of your choosing. Do not forget to close your diary file first by using the command ``diary diary.txt''. (If you are using your own computer, you can zip the files using any method you are familiar with.)

Extra credit

In this lab, values that you wanted to see were printed by Matlab automatically because the semicolon was left off the end of the lines, or because you used the Matlab dispcommand.

There is an additional command that is used for displaying results and that allows you a great deal of formatting flexibility. It is similar to the ``printf'' command in C and Java.

Exercise 9: Consider the following simple loop

for i=0:12

disp(['The square root of ',num2str(i^2),' is ',num2str(i)]);

end

1. Execute this loop. Note that the columns of numbers are not aligned.

2. Read the help message about the function fprintf. (In older versions of Matlab, you will find more information about format strings in the help message forsprintf.) Re-write the loop using fprintf so that the numbers that are printed are aligned so their final digits occur on a vertical line on the screen. Hint: If the ``fid'' parameter is omitted, then printing will go to the screen by default. Please include a copy of your fprintf command in your summary file.

3. Replace the square root with the tangent, so that the tangents of the numbers $0,1,4,9,\dots,144$ are printed and so the decimal points are aligned. Please include a copy of your fprintf command in your summary file.

4. Similarly, replace the tangent with the exponential, so that the exponentials of the numbers $0,1,4,9,\dots,144$ are printed and so the decimal points are aligned. Please include a copy of your fprintf command in your summary file.