May
18,2001
Homework
(Due:Final )
1) If a coefficient
matrix of a linear system of equations is in the following form (which is
called tridiagonal systems)
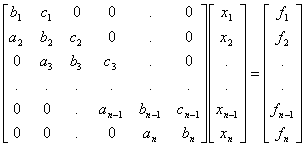 ,
,
for the solution of the
system above, a recursive method is introduced:
Elimination:
ai=ai/bi-1
bi=bi-ai*ci-1 i=2,n
fi=fi-ai*fi-1
Back substitution:
fn=fn/bn
fi=fi-ci*fi+1 i=n-1,1
As a result of the above
algorithm f will be the solution vector.
The following subroutine is given for the computer application:
subroutine
tridia(N,a,b,c,f)
IMPLICIT
REAL * 8 (A-H,O-Z)
DIMENSION
f(N),a(N),b(N),c(N)
Do
10 i=2,N
a(i)=a(i)/b(i-1)
b(i)=b(i)-a(i)*c(i-1)
10 f(i)=f(i)-a(i)*f(i-1)
f(n)=f(n)/b(n)
do
20 i=1,n-1
ii=n-i
20 f(ii)=(f(ii)-c(ii)*f(ii+1))/b(ii)
return
end
Find the cubic spline
functions for each interval and calculate approximate f values at x=0.2,0.6,1.2
for the following data. (Use the computer code given above in solving
tridiagonal matrix equation, HM=V) Take m0=mN=0.
|
Ý |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
X(i) |
0.1 |
0.3 |
0.5 |
0.7 |
0.9 |
1.1 |
1.3 |
|
F(xi) |
0.99750 |
0.97763 |
0.93847 |
0.88120 |
0.80752 |
0.71962 |
0.62009 |
2) Questions 1,2,3,5, 6, 7,10 in Exercise 6.