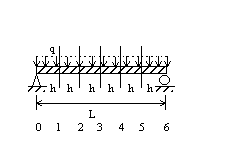ES305, COMPUTING METHODS IN ENGINEERING, FALL SEMESTER

EXERCISES 6

1) Solve the following differential equation using h=0.1 for two steps

a) by Euler’s method,

b) by Modified Euler’s (implicit) method

c) compare your results found in parts “a” and “b” and comment on the differences if any.

2) The governing differential equation of a SDOF (single degree of freedom) system given below with the corresponding initial conditions as

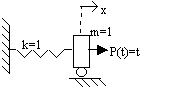
; x(0)=0, where .

Find the displacements at t= .01 and 0.02 seconds (i.e. h==0.01)

by using

i) Euler’s method for systems

ii) Runge Kutta’s method of order 2 for systems.

3) Consider, Governing Equation (GE) :

with the boundary Conditions (BC's): y (0) = 0, y (1) = 0

i) Solve the second order ordinary differential equation given above by Shooting method by subdividing the solution region 0 £ x £ 1 into 4 equal parts.

ii) Compare the results found in (i) with the results of the exact solution of this BVP given as

4) Given the following boundary value problem

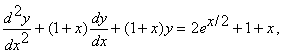
a) Show that the following matrix equation is the reduced form of the above boundary value problem by finite differences of order h² with h =0.25

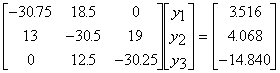
b) Solve the above matrix equation in part ‘a’ by LU decomposition.

5)

Figure shown on the left is the simple beam with the length of L, Modulus of Elasticity of E and Moment of Inertia of I. It is subjected to the uniformly distributed load q. Governing equation for this beam is:

and B.C. at x = 0 v = 0,

at x = L v = 0,

Where v is the lateral displacement and x is the horizontal axis. By using the formulas

and ,

obtain the linear system of equations for six divisions in terms of q, L, E, I. Solve the system by G.E.M. and compare the maximum displacement with the

(Find the actual error). At first, what can you do to decrease an error?